[Archive] Arithmétique des entiers relatifs [Ancien C1.III.4]

1. Nombres premiers entre eux

Dans la section [Arithmétique naturelle, Nombres premiers entre eux], nous avons introduit le plus grand commun diviseur de deux nombres entiers naturels, et la notion de nombres entiers naturels premiers entre eux.

Si l’algorithme d’Euclide nous a donné le moyen de « calculer » théoriquement le p.g.c.d de deux nombres entiers naturels, nous n’avons pas approfondi la question de comment déterminer théoriquement si deux nombres entiers naturels sont premiers entre eux. L’algorithme d’Euclide nous donne un moyen pratique (calculer le p.g.c.d !) mais il existe un critère théorique fondamental, le théorème de Bézout.

La raison pour laquelle nous avons reporté cette question ici, est que l’étude de la « primalité relative » est plus naturelle dans le contexte de l’ensemble $\mathbb Z$ des nombres entiers relatifs, même en ce qui concerne les entiers naturels. En fait, le théorème de Bézout s’énonce à partir des nombres entiers relatifs, même si l’on ne considère que des entiers naturels.

Nous reprenons donc ici l’étude des nombres premiers entre eux pour l’approfondir, en étendant les définitions adéquates déjà introduites pour les entiers naturels.

Nous commençons l’arithmétique des entiers relatifs par cette question, car elle nous permettra d’avancer sur la théorie des nombres premiers, où nous démontrerons le théorème de Gauss sur la décomposition en nombres premiers, grâce au lemme d’Euclide.

Définition 1
i) Si $m$ et $n$ sont deux entiers relatifs non tous deux nuls, le plus grand commun diviseur de $m$ et $n$ est le p.g.c.d de $|m|$ et $|n|$. On le note aussi $pgcd(m,n)$ ou encore $m\wedge n$.
ii) On dit que deux entiers relatifs $m$ et $n$ sont premiers entre eux, si $m\wedge n=1$.

Remarque 1
o) Le p.g.c.d de deux entiers relatifs $m$ et $n$ quelconques est donc toujours un entier naturel.
i) Cette définition est encore parfaitement analogue à la définition introduite pour les entiers naturels : le p.g.c.d des entiers relatifs $m$ et $n$ est ici encore le plus grand entier relatif $d$ tel que $d$ divise à la fois $m$ et $n$ (voir les exercices).
ii) Nous verrons dans cette section que le p.g.c.d de $m$ et $n$ est également un plus grand diviseur commun de $m$ et $n$ au sens de la divisibilité. Autrement dit, on a $m\wedge n|m,n$, et si $d\in\mathbb Z$ divise à la fois $m$ et $n$, alors $d$ divise $m\wedge n$. Or, cette propriété est également vraie de $-m\wedge n$, si bien que sur le plan de la divisibilité, l’ordre naturel dans $\mathbb Z$ n’est pas très pertinent : nous aurions pu définir un p.g.c.d de $m$ et $n$ comme un entier relatif ayant cette propriété. Comme il n’existe que deux tels entiers relatifs, on choisit le plus grand pour l’ordre naturel, c’est-à-dire celui qui est positif.

Voici le critère fondamental de primalité relative entre deux nombres entiers relatifs, que nous démontrons à l’aide de l’algorithme d’Euclide sur les nombres entiers naturels.

Théorème 1 [Bézout]
Si $m$ et $n$ sont deux entiers relatifs non nuls, alors il existe deux entiers relatifs $u$ et $v$ tels que $pgcd(m,n)=mu+nv$.

Démonstration
Supposons d’abord que $m,n\in\mathbb N$. On a soit $n\leq m$ soit $m\leq n$, et dans les deux cas on a $pgcd(m,n)=pgcd(n,m)$, donc quitte à intervertir $m$ et $n$ si nécessaire on peut supposer que $n\leq m$ (l’autre cas est traité de manière similaire), donc $m>0$. Soit $(r_i)_\mathbb N$ la suite obtenue à partir de l’algorithme d’Euclide appliqué à $m$ et $n$ (section [Arithmétique naturelle, Nombres premiers entre eux], op. cit.). Si $r_1=0$, on a $m=nq_1+r_1=nq_1$, donc $n|m$ et pour $u=0$ et $v=1$, on a bien alors $um+vn=n=pgcd(m,n)$. Si $r_1\neq 0$, par définition on a $m=nq_1+r_1$, d’où $r_1=m+n(-q_1)$ : par [Arithmétique naturelle, proposition 4], si $r_2=0$ on a $pgcd(m,n)=r_1$, qui est de la forme désirée. Supposons maintenant que $r_2\neq 0$, et soit $N$ le plus grand entier naturel $i\geq 2$ tel que $r_i\neq 0$, par [Arithmétique naturelle, lemme 8]. On suppose que pour tout $i=0,\ldots,N-1$, il existe $u_i,v_i\in \mathbb Z$ tels que $r_i=mu_i+nv_i$. Par définition, on peut écrire $r_{N-2}=r_{N-1}q_N+r_N$, d’où $r_N=r_{N-2}-r_{N-1}q_N=mu_{N-2}+nv_{N-2}-q_N(mu_{N-1}+nv_{N-1})=m(u_{N-2}-q_N u_{N-1})+n(v_{N-2}-q_N v_{N-1})$, qui est encore de la forme désirée. Par [Arithmétique naturelle, proposition 4] à nouveau, on a $r_N=pgcd(m,n)$, d’où le résultat dans ce cas.
En général, si $m,n\in\mathbb Z$, on a $|m|,|n|\in\mathbb N$ : par le cas précédent, il existe $u,v\in\mathbb Z$ tels que $pgcd(m,n)=pgcd(|m|,|n|)=|m|u+|n|v$. Par définition de la valeur absolue, il existe donc des entiers relatifs $u’,v’\in\mathbb Z$ tels que $pgcd(m,n)=mu’+nv’$. En effet, si $|m|=m$ et $|n|=n$, alors $u’=u$ et $v’=v$ conviennent; si $|m|=-m$ et $|n|=n$, alors $u’=-u$ et $v’=v$ conviennent; si $|m|=m$ et $|n|=-n$, alors $u’=u$ et $v’=-v$ conviennent; et si $|m|=-m$ et $|n|=-n$, alors $u’=-u$ et $v’=-v$ conviennent. $\square$

Remarque 2
L’essentiel de la démonstration porte sur le cas où $m,n\in\mathbb N$, et l’étude du second cas (où $r_1\neq 0$) montre que l’introduction des entiers relatifs est essentielle, puisqu’il faut utiliser l’opposition du quotient $q_1$ (dans le cas où $r_2=0$) ou une soustraction (dans le cas où $r_2\neq 0$).

Du théorème de Bézout on tire le critère théorique suivant, qui permet de caractériser les couples $(m,n)$ d’entiers relatifs premiers entre eux :

Corollaire 1
Deux entiers relatifs non nuls $m$ et $n$ sont premiers entre eux si et seulement si il existe $u,v\in\mathbb Z$ tels que $mu+nv=1$.

Démonstration
Par le théorème de Bézout (théorème 1), il existe $u,v\in\mathbb Z$ tels que $mu+nv=pgcd(m,n)$. Si $m$ et $n$ sont premiers entre eux, alors $pgcd(m,n)=1$, d’où l’égalité.
Inversement, si il existe $u,v\in\mathbb Z$ tels que $mu+nv=1$, notons $d=pgcd(m,n)$ : comme $d$ divise à la fois $m$ et $n$, il divise $mu+nv$, si bien que $d\mid 1$ et finalement, $d=1$ et $m$ et $n$ sont premiers entre eux. $\square$

Un autre corollaire du théorème de Bézout permet de déterminer quand une équation de la forme $ax+by=c$ possède des solutions entières en $x$ et $y$.

Corollaire 2
Si $m$, $n$ et $c$ sont trois entiers relatifs et $m$ et $n$ sont non nuls, alors l’équation $mx+ny=c$ possède une solution $(x,y)\in\mathbb Z^2$ si et seulement si $m\wedge n |c$.

Démonstration
Supposons que cette équation possède une solution $(u,v)\in\mathbb Z^2$, de sorte que l’on a l’égalité $mu+nv=c$ : comme $m\wedge n|m,n$, on a $m\wedge n|mu+nv=c$.
Réciproquement, si $m\wedge n|c$ il existe $k\in\mathbb Z$ tel que $c=k.(m\wedge n)$; par le théorème 1, soient $u,v\in\mathbb Z$ tels que $mu+nv=m\wedge n$ : on a $k.(mu+nv)=k.(m\wedge n)=c$, donc le couple $(ku,kv)$ est une solution de d’équation $mx+ny=c$. $\square$

La démonstration du théorème de Bézout montre qu’ici comme ailleurs, cela n’aurait pas trop de sens de séparer artificiellement l’arithmétique dans l’ensemble $\mathbb N$ de l’arithmétique dans l’ensemble $\mathbb Z$. Comme le montrera la section suivante, à propos de la décomposition en nombres premiers, il faut plutôt voir la seconde comme un « approfondissement » de la première.

Trouver une relation de Bézout entre deux entiers relatifs $m$ et $n$ non nuls, c’est trouver deux entiers relatifs $u$ et $v$ tels que $um+vn=pgcd(m,n)$. En utilisant la stratégie de la seconde partie de la démonstration du théorème de Bézout, il suffit de savoir le faire pour $m,n\in\mathbb N$.

Ceci peut se faire grâce à l’algorithme d’Euclide : écrivons le complètement pour deux entiers naturels $m\geq n>0$ comme dans la section [Arithmétique naturelle, Nombres premiers entre eux] (op. cit.). Nous définissons alors deux suites $(q_i)$ et $(r_i)$ d’entiers comme suit. On pose $n=r_0$, on écrit $m=nq_0+r_1$ la division euclidienne de $m$ par $n$ (donc avec $r_1<n$) et pour tout $n\geq 1$, on définit $q_n$ et $r_{n+1}$ en écrivant la division euclidienne de $r_{n-1}$ par $r_n$ sous la forme $r_{n-1}=r_nq_n+r_{n+1}$ (donc avec $r_{n+1}<r_n$).

Si on note $N$ l’indice du dernier reste non nul (par [Arithmétique naturelle, lemme 6]), on dispose ainsi de $N$ relations $m=nq_0+r_1$, $r_0=n=r_1q_1+r_2$, $r_1=r_2q_2+r_3$, … et $r_{N-2}=r_{N-1}q_{N-1}+r_N$. On en tire $r_1= m-nq_0$ et $r_2=n-r_1q_1=n-(m-nq_0)q_1=n(1+q_0q_1)+m(-q_1)$, puis $r_3=r_1-r_2q_2$, soit $r_3=(m-nq_0)-q_2(n(1+q_0q_1)+m(-q_1))=m(1+q_1q_2)+n(-q_0).(1+q_1q_2)$. De proche en proche, en substituant à $r_n$ la valeur obtenue par l’équation $r_{n-2}=r_{n-1}q_{n-1}+r_n$, soit $r_n=r_{n-2}-r_{n-1}q_{n-1}$, pour $n=2,\ldots,N$, on obtient une relation de Bézout entre $m$ et $n$.

Exemple 1
Cherchons une relation de Bézout entre $561$ et $-381$, en appliquant l’algorithme d’Euclide à $m=561$ et $n=385$. On obtient $561=385.1+176$, $385=176.2+33$, $176=33.5+11$ et $33=11.3$. On en tire $176=561-385$ et $33=385-176.2=385-(561-385).2=561.(-2)+385.3$. On a également $11=176-33.5=(561-385)-(385.3-561.2).5=561.11+385.(-16)$, relation de Bézout entre $561$ et $385$, puisque $11=pgcd(561,385)=pgcd(561,-385)$. On en déduit la relation de Bézout $561.11+(-385).16=11$.

La figure suivante donne une interprétation géométrique du théorème de Bézout basée sur la géométrie affine (voir le chapitre 4).

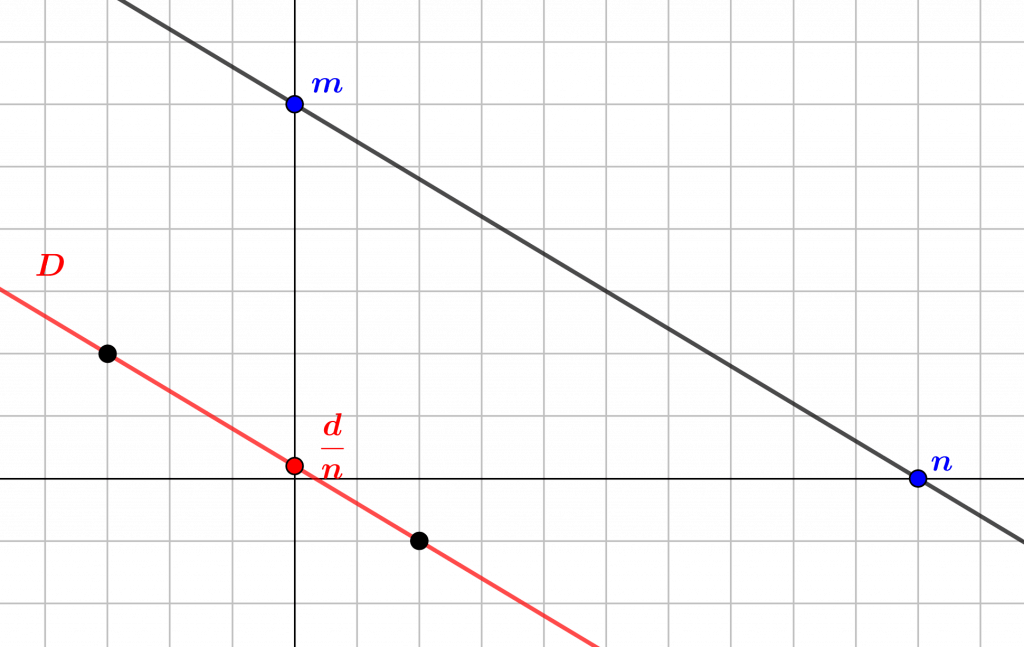
La fin de cette section est consacrée à établir le lemme de Gauss (théorème 2), qui est « l’instrument » essentiel du lemme d’Euclide (lemme 2), et donc du théorème de Gauss sur la décomposition des entiers relatifs en facteurs premiers.

Proposition 1
Si $m,n$ et $p$ sont trois entiers relatifs non nuls, alors :
i) $m\wedge n$ est un plus grand diviseur commun de $m$ et $n$ au sens de $|$; autrement dit, pour tout $d\in\mathbb Z$ tel que $d|m,n$, on a $d|m\wedge n$
ii) On a $|p|\times(m\wedge n)=(p\times m)\wedge (p\times n)$.

Démonstration
i) Par le théorème de Bézout (théorème 1), il existe $u,v\in\mathbb Z$ tels que $m\wedge n=mu+nv$. Supposons que $d\in \mathbb Z$ est un diviseur commun de $m$ et $n$ : on a $d|mu,nv$, donc $d|mu+nv=m\wedge n$.
ii) Si $d\in \mathbb Z$ et $d|m,n$, alors on a $pd|pm,pn$, d’où $pd|(pm\wedge pn)$ par (i); en particulier, on a $p\times (m\wedge n)|(pm\wedge pn)$. Inversement, comme $p|pm\wedge pn$ puisque $p|pm,pn$, il existe $q\in\mathbb Z$ tel que $pq=pm\wedge pn$, donc aussi $pq|pm$ et $pq|pn$ : il existe $u,v\in \mathbb Z$ tels que $pm=upq$ et $pn=vpq$, d’où $p(m-uq)=0$ et $p(n-vq)=0$, si bien que $m=uq$ et $n=vq$ par intégrité ([Axiomes et structure de l’ensemble $\mathbb Z$, théorème 1]), et finalement $q|m,n$. Par (i) à nouveau, on a $q|m\wedge n$, d’où $pm\wedge pn=pq|p\times (m\wedge n)$. Par conséquent, on a à la fois $p\times (m\wedge n)|pm\wedge pn$ et $pm\wedge pn|p\times(m\wedge n)$, d’où $p\times (m\wedge n)=pm\wedge pn$ ou $p\times (m\wedge n)=-(pm\wedge pn)$, soit $|p|\times (m\wedge n)=|p\times(m\wedge n)|=(p\times m)\wedge (p\times n)$ (le second membre de l’égalité est toujours positif). $\square$

Remarque 3
Lorsque $m,n,p\in\mathbb N$, on peut supprimer les valeurs absolues dans (ii).

Théorème 2 [Lemme de Gauss]
Si $m,n$ et $p$ sont des entiers relatifs non nuls, et si $m$ divise $np$ et $m$ et $n$ sont premiers entre eux, alors $m$ divise $p$.

Démonstration
Par la proposition 1(ii), on a $mp\wedge np=|p|\times(m\wedge n)$ et comme $m\wedge n=1$, on en déduit que $mp\wedge np=|p|$. Mais $m|np$ par hypothèse, si bien que $m|(mp\wedge np)=|p|$ par la proposition 1(i), donc $m|p$ également. $\square$

Remarque 4
Ici, le contenu essentiel du théorème a déjà été traité dans la proposition 1.

1.1. Exercices

Exercice 1
i) Si $m$ et $n$ sont deux entiers relatifs non tous deux nuls, démontrer que le p.g.c.d $m\wedge n$ de $m$ et $n$ est le plus grand entier relatif $d$ tel que $d$ divise à la fois $m$ et $n$, autrement dit que $d|m,n$ et que si $k\in\mathbb Z$ et $k|m,n$, alors $k\leq d$.
ii) Trouver une relation de Bézout entre $63$ et $-175$.
iii) Montrer que $77$ divise $15400$ et que $77$ et $39$ sont premiers entre eux. En déduire que $77$ divise $385$.

2. Nombres premiers