[Archive] Arithmétique des nombres rationnels [Ancien C1.III.6]

1. Décomposition multiplicative et valuations $p$-adiques

Dans cette section et jusqu’à la fin du chapitre, nous abordons l’extension de propriétés arithmétiques de l’ensemble $\mathbb Z$ à l’ensemble $\mathbb Q$. Mais puisque en axiomatisant cet ensemble, nous avons ajouté des inverses multiplicatifs à tout élément non nul, par [Axiomes et structure de l’ensemble $\mathbb Q$, proposition 9] tout nombre rationnel $q$ est divisible par tout nombre rationnel non nul $r$ ! Cela signifie que la relation de divisibilité ne présente plus aucun intérêt arithmétique dans l’ensemble $\mathbb Q$, or nous avons défini l’arithmétique dans $\mathbb N$ et dans $\mathbb Z$ comme l’étude de cette relation…

En fait, l’existence des décompositions en nombres premiers subsiste de manière essentielle dans la théorie des nombres rationnels, et on l’étudie en rapport à des « raffinements » associés à chaque nombre premier et obtenus à partir de l’extension de la notion d’exposant évoquée à la section [Arithmétique des entiers relatifs :: Nombres primaires], laquelle nécessite de définir auparavant les puissances négatives d’un nombre rationnel.

1.1. Puissances des nombres rationnels

Dans la section [Arithmétique des entiers relatifs :: Puissances des entiers relatifs], nous avons défini proprement la puissance d’un nombre entier relatif par un entier naturel quelconque. Nous allons définir ici la puissance d’un nombre rationnel par un entier relatif.

Définition 1
Soit $r$ un nombre rationnel.
A) Si $n$ est un nombre entier naturel, on définit le nombre rationnel $r$ (à la) puissance $n$, noté $r^n$, par récurrence, de la manière suivante :
i) Si $n=0$, on pose $r^0=1$
ii) On pose $r^{n+1}:=r^n.r$, en supposant que $r^n$ est défini
B) Si $r$ est non nul et $n$ est un nombre entier négatif, on définit le nombre rationnel $r^n$ comme $1/r^{-n}$.

La définition de la puissance d’un nombre rationnel par un entier naturel est exactement la même que celle de la puissance d’un nombre entier relatif : elle prolonge donc celle-ci et c’est celle que nous adopterons aussi pour les nombres réels et les nombres complexes.

L’extension de la définition consiste principalement à définir les puissances négatives à partir de l’inversion. Cette définition est justifiée dans la mesure où pour tout nombre rationnel $r\neq 0$ et tout entier $n\leq 0$, l’entier $-n$ est positif, et le nombre rationnel $r^{-n}$ est donc bien défini par récurrence et différent de zéro.

Il faut prendre garde toutefois que la puissance n’est pas toujours définie pour $r=0$, puisque $0^1=0$, et donc que $0^{-1}$ n’a pas de sens. C’est en fait le seul cas où $r^n$ ne peut pas être défini pour $n<0$.

Les propriétés des puissances entières des nombres rationnels sont essentiellement les mêmes que dans le cas des nombres entiers (évoquées dans [Arithmétique des entiers relatifs, proposition 2]) :

Proposition 1
Soient $q$ et $r$ des nombres rationnels, et $m,n$ des entiers relatifs. Lorsque les puissances sont toutes définies, on a :
i) $(q.r)^{m}=q^m.r^m$
ii) $q^{m+n}=q^m.q^n$
iii) $(q^m)^n=q^{m.n}$.

Démonstration
Lorsque $m,n\geq 0$, les puissances sont toujours définies et les démonstrations sont identiques à celles de la démonstration de [Arithmétique des entiers relatifs, proposition 2] (op. cit.) : nous ne les reproduisons pas ici. On traite donc du cas où l’un des nombres $m$ et $n$ est strictement négatif, et par symétrie on peut choisir $m<0$.
i) On a $(q.r)^m=1/(q.r)^{-m}$ (par définition) $=1/(q^{-m}.r^{-m})$ (par le cas $m>0$) $=(1/q^{-m}).(1/r^{-m})=q^m.r^m$ (par définition).
ii) On distingue deux cas, selon que $m+n\geq 0$ ou que $m+n<0$. Supposons que $m+n\geq 0$, posons $k=m+n$ et raisonnons par récurrence sur $k$. Si $k=0$, on a $m=-n$, et $q^{m+n}=q^k=q^0=1=(q^m).(1/q^m)=q^m.q^{-m}=q^m.q^n$ et la propriété est vérifiée. Supposons qu’elle le soit au rang $k$, et que $m+n=k+1$ : comme $m<0$, on a $n>0$, donc on peut écrire $n$ sous la forme $n=l+1$, d’où $m+l=k$, et on a alors $q^{m+n}=q^{k+1}=q^{m+l+1}=q^{m+l}.q$ (par définition) $=(q^m.q^l).q$ (par hypothèse de récurrence appliquée à $m+l=k$) $=q^m.q^{l+1}=q^m.q^n$, et la propriété est vérifiée au rang $k+1$. Par récurrence, elle l’est pour tout $k\in\mathbb N$, donc pour tous $m,n$ tels que $m<0$ et $m+n\geq 0$.
Supposons maintenant que $m+n<0$, et distinguons à nouveau deux cas, selon que $n\leq 0$ ou $n> 0$. Si $n\leq 0$, on a $q^{m+n}=1/q^{-m-n}$ (par définition) $=1/(q^{-m}.q^{-n})$ (par le cas $m,n\geq 0$) $=(1/q^{-m}).(1/q^{-n})=q^m.q^n$. Si $n>0$, on a $-n<0$ et : comme $-m-n>0$, par le cas $m+n\geq 0$ et en échangeant les rôles de $n$ et de $-m$, on obtient également $q^{m+n}=1/q^{-m-n}=1/(q^{-m}.q^{-n})=(1/q^{-m}).(1/q^{-n})=q^m.q^n$.
iii) On a $(q^m)^n=(1/q^{-m})^n$ (par définition d’une puissance négative) $=(1/q)^{-mn}$ (par le cas $m,n\geq 0$) $=q^{mn}$. $\square$

Notons que par définition, si $r$ est un nombre rationnel non nul, on a $r^{-1}=1/r$, et donc pour tout entier naturel $n$, $(1/r)^n=(r^{-1})^n=r^{-n}=1/r^n$ par la proposition 1.

1.2. Valuations $p$-adiques

La factorisation des entiers naturels (et donc des entiers relatifs) en produit de puissances de nombres premiers par le théorème de Gauss ([Arithmétique des entiers relatifs, théorème 4]) peut dans un certain sens s’étendre aux nombres rationnels.

Il existe au moins deux façons de le faire : nous commençons par exposer la plus simple, qui consiste à décomposer le numérateur $a$ et le dénominateur $b$ d’une représentation $a/b$ d’un nombre rationnel en nombres premiers $p_1,\ldots,p_n$, et à réécrire la fraction $a/b$ sous la forme d’un produit de ces facteurs premiers, avec des puissances positives ou négatives.

En sélectionnant un des nombres premiers $p_i$ de cette décomposition « multiplicative », nous pouvons alors considérer le nombre $a/b$ « relativement au nombre $p_i$ », ce qui permet d’en tirer des informations arithmétiques intéressantes. Or, si $p\in\mathbb N$ est un nombre premier, nous avons défini dans la section [Arithmétique des entiers relatifs :: Nombres primaires] (op. cit.) l’exposant de $p$ dans un entier relatif non nul. Nous pouvons utilement étendre cette notion à tout nombre rationnel non nul de la manière suivante :

Définition 2
Si $r=a/b$ est un nombre rationnel non nul, la valuation $p$-adique de $r$ est le nombre entier relatif $v_p(r)=v_p(a)-v_p(b)$, où $v_p(a)$ est l’exposant de $p$ dans $a$.

Remarque 1
La valuation ne peut être définie que pour un nombre rationnel non nul, puisque si $a=0$, l’exposant de $p$ dans $a$ n’est pas défini.

A priori, la valuation $p$-adique pourrait dépendre du choix d’une représentation d’un rationnel non nul.

Pour montrer qu’elle ne dépend pas d’un tel choix et qu’elle est donc bien définie, supposons que $r=a/b=c/d$ : on a $ad=bc$ dans $\mathbb Z$, donc par [Arithmétique des entiers relatifs, proposition 3], $v_p(a)+v_p(d)=v_p(ad)=v_p(bc)=v_p(b)+v_p(c)$, si bien que $v_p(a)-v_p(b)=v_p(c)-v_p(d)$, et $v_p(r)$ est bien définie.

Aussi, notons que si $n\in\mathbb Z$, on a $v_p(n/1)=v_p(n)-v_p(1)=v_p(n)$ pour tout entier naturel premier $p$, puisque $p$ ne divise pas $1$, si bien que la valuation $p$-adique d’un entier non nul $n$ vu comme le nombre rationnel $1/n$ est l’exposant de $p$ dans $n$ : les valuations $p$-adiques sont les prolongements des exposants de $\mathbb Z^*$ à $\mathbb Q^*$.

Tout comme l’exposant « transforme » la multiplication des entiers relatifs non nuls en l’addition des entiers naturels, la valuation « transforme » la multiplication des rationnels non nuls en l’addition des entiers relatifs.

Cette propriété est regroupée avec les propriétés élémentaires des valuations $p$-adiques dans la proposition suivante. Toutes ces propriétés sont analogues de celles de la valeur absolue (section [Axiomes et structures de l’ensemble $\mathbb Q$ :: La valeur absolue]), pour des raisons profondes qui dépassent le cadre de ce cours.

Proposition 2
Pour tous nombres rationnels non nuls $r$ et $s$, on a :
i) $v_p(1)=0$
ii) $v_p(r.s)=v_p(r)+v_p(s)$
iii) $v_p(r+s)\geq \min\{v_p(r),v_p(s)\}$.

Démonstration
i) On a $v_p(1)=v_p(1/1)=v_p(1)-v_p(1)=0$.
ii) Ecrivons $r=a/b$ et $s=c/d$ : on a $v_p(r.s)=v_p(ac/bd)=v_p(ac)-v_p(bd)$ (par définition) $=v_p(a)+v_p(c)-v_p(b)-v_p(d)$ (par [Arithmétique des entiers relatifs, proposition 3], op. cit.) $=(v_p(a)-v_p(b))+(v_p(c)-v_p(d))=v_p(r)+v_p(s)$.
iii) Avec les mêmes notations, nous voulons montrer que $v_p(ad+bc)-v_p(bd)\geq \min\{v_p(a)-v_p(b),v_p(c)-v_p(d)\}$. En réécrivant $v_p(bd)=v_p(b)+v_p(d)$, distinguons deux cas, selon la valeur du minimum $m:=\min\{v_p(a)-v_p(b),v_p(c)-v_p(d)\}$ au membre de droite de l’inégalité à démontrer. Si $m=v_p(a)-v_p(b)$, nous voulons montrer que $v_p(ad+bc)-v_p(b)-v_p(d)\geq v_p(a)-v_p(b)$, ou encore en ajoutant $v_p(b)+v_p(d)$ aux deux membres, que $v_p(ad+bc)\geq v_p(a)+v_p(d)=v_p(ad)$. Or, par définition on a $p^{v_p(ad)}|ad$ et comme $v_p(a)-v_p(b)\leq v_p(c)-v_p(d)$, on a $v_p(ad)=v_p(a)+v_p(d)\leq v_p(c)+v_p(b)=v_p(bc)$, d’où aussi $p^ {v_p(ad)}|bc$, si bien que finalement, on a $p^{v_p(ad)}|ad+bc$, d’où $v_p(ad+bc)\geq v_p(a)+v_p(d)$, par définition de l’exposant de $p$ dans $ad+bc$. Si $m=v_p(c)-v_p(d)$, on raisonne exactement de la même manière en échangeant les rôles de $(a,b)$ et de $(c,d)$. $\square$

La valuation $p$-adique d’un nombre rationnel non nul est toujours un entier relatif. Grâce à cette notion, on peut établir la décomposition multiplicative d’un nombre rationnel strictement positif comme généralisation de la décomposition d’un entier naturel en nombres premiers.

Lemme 1
Soient $r$ un nombre rationnel strictement positif, et $(a,b)$ sa forme irréductible canonique. Si $p$ est un entier naturel premier, alors :
i) On a $v_p(r)=0$ si et seulement $p$ ne divise ni $a$, ni $b$
ii) On a $v_p(r)>0$ si et seulement si $p|a$ mais $p\nmid b$, et alors $v_p(r)=v_p(a)$
iii) On a $v_p(r)<0$ si et seulement si $p|b$ mais $p\nmid a$, et alors $v_p(r)=-v_p(b)$.

Démonstration
i) Par définition, on a $v_p(r)=v_p(a)-v_p(b)$, donc si $v_p(r)=0$, on a $v_p(a)=v_p(b)$ : si $v_p(a)>0$, alors $p|a$ et $p|b$, ce qui contredit la primalité relative de $a$ et $b$, d’où $p\nmid a$ et $p\nmid b$. Inversement, si $p$ ne divise ni $a$, ni $b$, on a $v_p(r)=v_p(a)-v_p(b)=0-0=0$.
ii) Supposons que $v_p(r)>0$ : si $b|p$, on a $v_p(a)>v_p(b)>0$, donc $p|a$ également, ce qui est impossible à nouveau puisque $pgcd(a,b)=1$. On en déduit que $p\nmid b$, $v_p(b)=0$, et $v_p(r)=v_p(a)-v_p(b)=v_p(a)$.
Inversement, si $p|a$ on ne peut avoir $p|b$ par primalité relative, donc on a $v_p(r)=v_p(a)>0$.
iii) Supposons que $v_p(r)<0$ : si $a|p$, on a $v_p(b)>v_p(a)>0$, donc $p|b$ également, ce qui est impossible, d’où $p\nmid a$, $v_p(a)=0$, et $v_p(r)=v_p(a)-v_p(b)=-v_p(b)$. La réciproque se démontre de manière évidente. $\square$

Dans le théorème suivant, qui prolonge le théorème de Gauss ([Arithmétique des entiers relatifs, théorème 4], op. cit.), nous utilisons une notation nouvelle pour le produit d’un nombre fini de nombres rationnels. La notation est analogue à celle des sommes finies (section [Arithmétique des entiers relatifs :: Critères de divisibilité]), sauf qu’on ajoute à l’indexation (ici $i$ variant de $1$ à $n$) une condition sur les indices (ici $v_{p_i}(r)>0$ ou $v_{p_i}(r)<0$). Ceci signifie qu’on effectue le produit des nombres indexés par $i$, en ne retenant que ceux pour lesquels la condition sur l’indice $i$ est vérifiée. En toute rigueur nous devrions définir intégralement le procédé, ce que nous ferons plutôt dans un cours ultérieur : la notation est ici suffisamment claire.

Théorème 1
Si $r$ est un nombre rationnel strictement positif, il existe un entier naturel $n$ et des nombres premiers $p_1<\ldots <p_n$ uniques, ainsi que des entiers relatifs non nuls $k_1,\ldots,k_n$ uniques, tels que $r=p_1^{k_1}\ldots p_n^{k_n}$. De plus, les nombres $k_i$ sont les $v_{p_i}(r)$.

Démonstration
Si $r=1$, alors $n=0$ convient : la décomposition est « vide ».
Si $r\neq 1$, écrivons $r=a/b$ sous forme irréductible canonique, c’est-à-dire avec $b>0$ et $a$ et $b$ premiers entre eux, de sorte que $a\neq b$. Soient $n\in\mathbb N$ et $p_1<\ldots <p_n$ les nombres premiers apparaissant avec un exposant non nul soit dans la décomposition de $a$ en nombres premiers, soit dans celle de $b$. Par le lemme 1, pour tout $i=1,\ldots,n$ on a $v_{p_i}(r)\neq 0$, et $a=\prod_{i,v_{p_i}>0} p_i^{v_{p_i}(r)}$ et $b=\prod_{i,v_{p_i}(r)<0} p_i^{-v_{p_i}(r)}$, d’où $r=a/b=\prod_i p_i^{v_{p_i}(r)}$, et l’existence de la décomposition est démontrée.
Concernant l’unicité de la décomposition, supposons que $r=p_1^{k_1}\ldots p_n^{k_n}$ avec $p_1<\ldots <p_n$ des entiers naturels premiers et $k_i\in\mathbb Z^*$ pour tout $i=1,\ldots,n$, et soit à nouveau $(a,b)$ la forme irréductible canonique de $r$. Par le lemme 1, les nombres premiers $p_i$, $i=1,\ldots,n$, sont les facteurs premiers de $a$ ou de $b$, et pour tout $i=1,\ldots,n$ on a $k_i=v_{p_i}(r)$, si bien que la décomposition est unique. $\square$

Exemple 1
Décomposons le nombre rationnel $r=6375/1485$ en nombres premiers. Le numérateur et le dénominateur sont divisibles par $5$, on peut donc simplifier en $r=1275/297$. Deux décompositions en nombres premiers donnent $1275=3.5^2.17$ et $297=3^3.11$, donc la décomposition cherchée est $r=3^{-2}.5.11^{-1}.17$.

La figure suivante propose une interprétation graphique de la décomposition d’un nombre rationnel positif en puissances de nombres premiers.

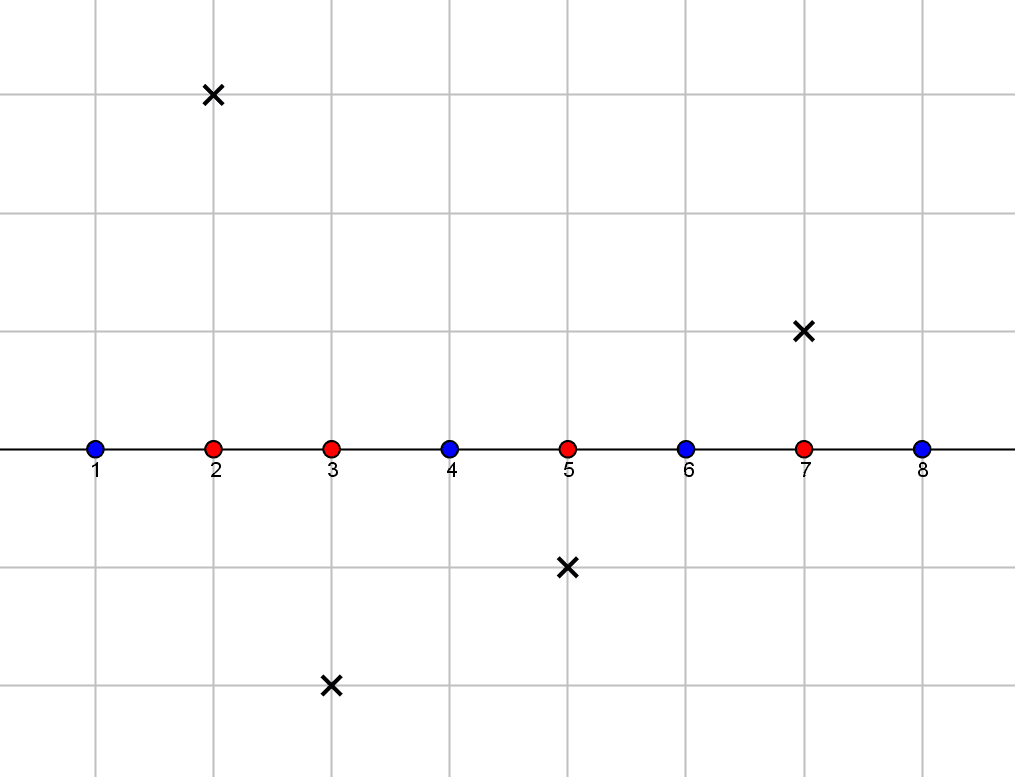
Grâce à la notion de valuation, on peut aussi redémontrer de manière élémentaire que le nombre réel $\sqrt 2$ n’est pas rationnel :

Proposition 3
Il n’existe aucun nombre rationnel $r$ tel que $r^2=2$.

Démonstration
Supposons par l’absurde qu’il existe $r\in\mathbb Q$, nécessairement non nul, tel que $r^2=2$. On considère alors la valuation $2$-adique de $2$, qui vaut $1$ puisque $1$ est l’exposant de $2$ dans $2$. Par la proposition 2, on peut aussi écrire $v_2(r^2)=v_2(r.r)=v_2(r)+v_2(r)=2v_2(r)$. Il s’ensuit que $1=2v_2(r)$, soit $v_2(r)=\frac{1}{2}$, ce qui est impossible puisque la valuation $2$-adique est toujours un entier relatif. Par reductio ad absurdum, on en déduit qu’il n’existe pas de racine carrée de $2$ dans l’ensemble $\mathbb Q$. $\square$

L’élément déterminant dans la démonstration de la proposition 3 est le caractère impair de l’exposant de $2$ (sa valuation $2$-adique comme nombre rationnel) dans le nombre entier $2$. Cette idée permet en fait de caractériser tous les nombres rationnels qui possèdent une racine carrée dans $\mathbb Q$.

Théorème 2
Un nombre rationnel $r$ possède une racine carrée dans $\mathbb Q$ si et seulement si il est positif et pour tout entier naturel premier $p$, l’entier relatif $v_p(r)$ est pair.

Démonstration
Si $r<0$, alors comme le carré d’un nombre rationnel est toujours positif par [Axiomes et structure de l’ensemble $\mathbb Q$, proposition 12], $r$ ne peut avoir de racine carrée; par contraposée un nombre rationnel possédant une racine carrée est toujours positif.
Si $r=0$, on a $r=0^2$, donc $r$ possède une racine carrée. Supposons désormais que $r> 0$ et décomposons $r$ en facteurs premiers sous la forme $p_1^{v_{p_1}(r)}\ldots p_n^{v_{p_n}(r)}$ par le théorème 1. Si pour tout entier naturel premier $p$, l’entier $v_p(r)$ est pair, en particulier pour $i=1,\ldots,n$ $v_{p_i}(r)$ est pair, on peut l’écrire sous la forme $v_{p_i}(r)=2k_i$, $k_i\in\mathbb Z$. Le nombre rationnel $q=p_1^{k_1}\ldots p_n^{k_n}$ est alors une racine carrée de $r$, puisque $q^2=p_1^{2k_1}\ldots p_n^{2k_n}=r$.
Réciproquement, si $r$ possède une racine carrée rationnelle $s$, on peut supposer que $s>0$ (car si $s<0$, on a $-s>0$ et $(-s)^2=s^2=r$, donc on peut toujours en tirer une racine carrée positive). Décomposons $s$ en facteurs premiers sous la forme $q_1^{l_1}\ldots q_m^{l_m}$, avec $q_1<\ldots <q_m$ et $v_{q_j}(s)=l_j\in\mathbb Z^\times$ pour tout $j$ : on a $s^2=q_1^{2l_1}\ldots q_m^{2l_m}=r$, donc par unicité de la décomposition de $r$ (théorème \ref{DECOMPQ}) on a $\{q_1,\ldots,q_m\}=\{p_1,\ldots,p_n\}$ et la valuation $p_i$-adique $v_{p_i}(r)=2l_i$ de $r$ est paire pour tout $i=1,\ldots,n$. Puisque la valuation $p$-adique de $r$ est nulle pour tous les autres entiers naturels premiers $p$ par le lemme 1, elle est paire pour tous les nombres premiers. $\square$

1.4. Exercices

Exercice 1
i) Démontrer par récurrence que pour tout entier naturel premier $p$, pour tout nombre rationnel non nul $r$ et pour tout entier naturel $m$, on a $v_p(r^m)=m.v_p(r)$. En déduire que pour tout entier naturel premier $p$ et pour tout entier naturel $m>1$, $p$ n’a pas de racine $m$-ième dans $\mathbb Q$ (c’est-à-dire qu’il n’existe pas de nombre rationnel $r$ tel que $r^m=p$).
ii) Soit $r$ un nombre rationnel non nul. Montrer que $v_p(r)=v_p(|r|)$ pour tout entier naturel premier $p$.
iii) Démontrer la réciproque de la clause (iii) du lemme 1.

Problème 1
L’objectif de ce problème est de généraliser le théorème 2 sous la forme suivante : si $m$ est un entier naturel $>1$ et $r$ un rationnel non nul, alors $r$ possède une racine $m$-ième dans $\mathbb Q$ (c’est-à-dire : il existe un rationnel $s$ tel que $s^m=r$) si et seulement si on se trouve dans l’un des deux cas (mutuellement exclusifs) suivants :
– $m$ est pair, $r>0$ et $m|v_p(r)$ pour tout nombre premier $p$
– $m$ est impair et $m|v_p(r)$ pour tout nombre premier $p$.
A) On suppose d’abord que $m$ est pair.
i) Montrer que si $r<0$, $r$ ne possède pas de racine $m$-ième dans $\mathbb Q$.
ii) Montrer que si $r>0$, alors $r$ possède une racine $m$-ième dans $\mathbb Q$ si et seulement si $m|v_p(r)$ pour tout nombre premier $p$.
B) On suppose désormais que $m$ est impair.
iii) Montrer que si $r\neq 0$ et $m|v_p(r)$ pour tout nombre premier $p$, et si $p_1^{k_1}\ldots p_n^{k_n}$ est la décomposition de $|r|$ en facteurs premiers, alors pour $s:=p_1^{k_1/m}\ldots m_n^{k_1/m}$, on a $(|r|/r)^m.s^m=r$.
iv) Montrer que si $r\neq 0$ et $r$ possède une racine $m$-ième $s$ dans $\mathbb Q$, alors $m|v_p(r)$ pour tout nombre premier $p$.
C) Conclure, sans oublier de traiter le cas où $r=0$.

2. Commensurabilité