The representation of the Euclidean plane as the Cartesian product \(\mathbb R^2\) allows us to decompose any vector of the plane into two coordinates, its abscissa and its ordinate. This decomposition is linked to a particular and natural “representation system”, which is called a base. There are an infinite number of such bases, and among them an infinite number of so-called orthonormal bases.
1. The canonical basis and the bases of the Euclidean plane
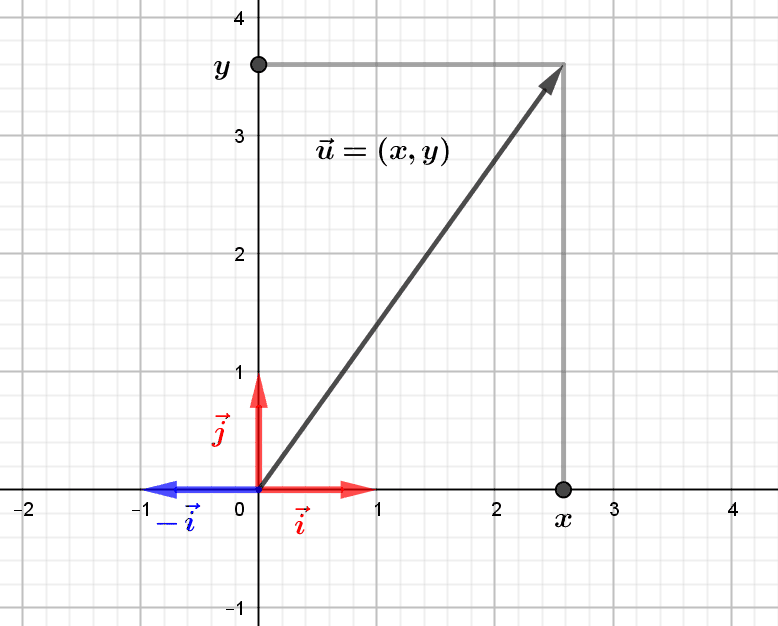
1.1. The natural representation of a vector in the canonical basis
Any vector \((x,y)\) of the Euclidean plane is represented as \((x,y)=x.(1,0)+y. (0,1)\), and this in a unique way: if \((x,y)=u.(1,0)+v.(0,1)\), then \((x,y)=(u,0)+(0,v)=(u,v)\), therefore \(x=u\) and \(y=v\). We say that the vectors \(\vec i=(1,0)\) and \(\vec j=(0,1)\) form the canonical basis \((\vec i,\vec j)\) of the Euclidean plane \(\mathbb R^2\). The real numbers \(x\) and \(y\), abscissa and ordinate of the vector \(\vec u=(x,y)\), are the coordinates of the vector \(\vec u\) in this canonical basis. However, although this way of decomposing a vector in the canonical basis is completely natural, it is possible to perform such a decomposition in a multitude of other “representation systems”, called bases, of the Euclidean plane.
1.2. Problem: describe the other bases of the Euclidean plane
It is often useful to be able to change the representation system, for example when describing a movement by a curve. In this case, one chooses a representation system associated with the moving point described by the curve, and possessing interesting geometrical properties. In this article we want to describe properly what the bases of the plane are, and introduce in a rigorous way the fundamental notion of orthonormal basis.
2.Describing the bases of the plane by a simple analytical criterion
2.1. The direction of a non-zero vector
We can understand the notion of base in the plane in a simple way, from that of the direction of a non-zero vector. If \(\vec u=(a,b)\) is a non-zero vector, it indeed determines a vector line, which is the set of vectors \(\vec v=(x,y)\) which are proportional to \(\vec u=(x,y)\), in other words which have the form \(\vec u\), that is \((x,y)=(\lambda.a,\lambda.b)\). This line is the direction of the vector \(\vec u\), and it is easy to show that any vector \(\vec v=(x,y)\) is on this line if and only if the equation \[(*)\ -bx+ay=0\] is verified.
2.2. Pairs of non-zero and collinear vectors
This being established, we say that two non-zero vectors \(\vec u=(a,b)\) and \(\vec v=(c,d)\) are collinear (i.e. parallel) if they have the same direction, i.e. determine the same line \(D\). This is exactly the same as saying that \(\vec v\) is on the direction of \(\vec u\), in other words that the equation \(-bc+ad=0\) is verified, thanks to condition \((*)\). Now, in such a case, any linear combination of \(\vec u\) and \(\vec v\), i.e. any vector of the form \(\vec w=\alpha.\vec u+\beta.\vec v\), with coefficients \(\alpha,\beta\in\mathbb R\), is necessarily also on the line \(D\). Indeed, we can write \(\vec w=(\alpha.a,\alpha.b)+(\beta.c,\beta.d)=(\alpha.a+\beta.c,\alpha.b+\beta.d)\), and check for example that \(-b.(\alpha.a+\beta.c)+a.(\alpha.b+\beta.d)=0\). In other words, if \(\vec u\) and \(\vec v\) are collinear, it is impossible to “decompose” vectors other than those of \(D\) from \(\vec u\) and \(\vec v\) !
2.3. Characterising the bases of the plane by collinearity
Thus, to obtain a “basis” of the plane, i.e. a system of representation in coordinates for all the vectors of the plane, it is necessary to choose at least two non-zero and non-collinear vectors \(\vec u=(a,b)\) and \(\vec v=(c,d)\). One can then show that any vector \(\vec w=(x,y)\) of the plane \(\mathbb R^2\) decomposes in a unique way in terms of \(\vec u\) and \(\vec v\), i.e. that there exists a unique pair of real numbers \(\alpha,\beta)\) such that \(\vec w=\alpha. \vec u+\beta.\vec v\). In fact, to say that \(\vec u\) and \(\vec v\) are not colinear, is to say now that \(-bc+ad\neq 0\), i.e. that \(ad-bc\neq 0\). We then solve a system of two equations with two unknowns translating this equality, namely \[\left\lbrace\begin{array}{ccc} x & = & \alpha.a + \beta.b\\y & = & \alpha.c + \beta.d.\end{array}\right.\] We find \(\alpha=\dfrac{1}{ad-bc}.(dx-cy)\) and \(\beta=\dfrac{1}{ad-bc}.(ay-bx)\), and we can check by calculation that we obtain a decomposition of \(\vec w\), which one can show is unique.

3.Orthonormal bases
3.1. Orthogonal and unitary vectors
Among the bases of the plane \((\vec u,\vec v)\), we distinguish those which determine vectorial isometries, and which have two particular properties:
1. The vectors \(\vec u\) and \(\vec v\) are orthogonal, that is to say that their scalar product is null.
2. The vectors\(\vec u\) and \(\vec v\) are unitary, i.e. of norm \(1\).
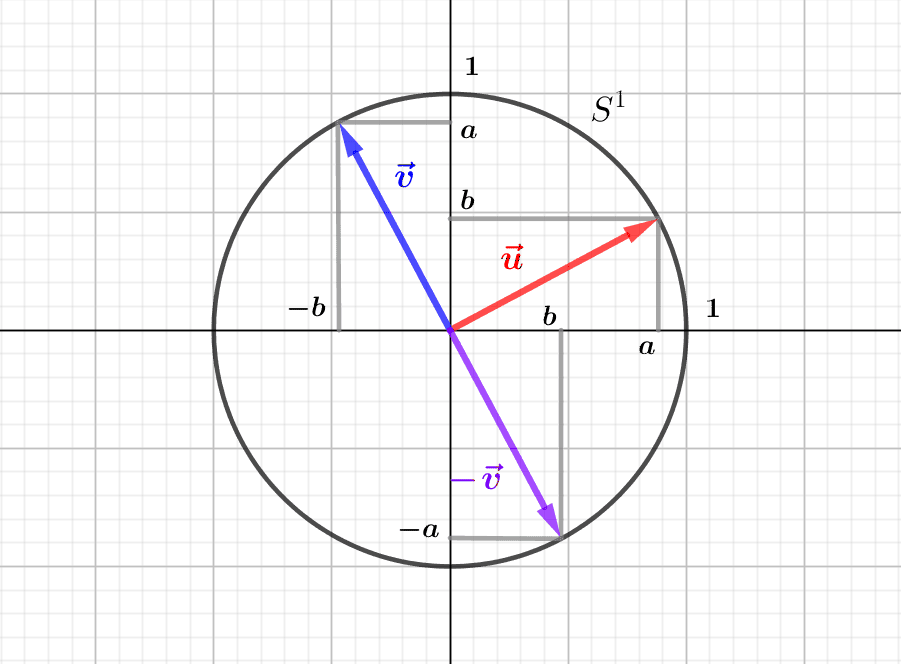
Let us write \(\vec u=(a,b)\) and \(\vec v=(c,d)\), and let us give an analytical characterisation of these two properties. The vectors \(\vec u\) and \(\vec v\) are orthogonal if and only if \(\vec u.\vec v=ac+bd=0\), and they are unitary if and only if \(||\vec u||=||\vec v||=1\), that is to say \(\sqrt{a^2+b^2}=\sqrt{c^2+d^2}=1\), or again \(a^2+b^2=c^2+d^2=1\). An orthonormal basis is therefore formed by “perpendicular” vectors located on the trigonometric circle.
3.2. Direct and indirect orthonormal bases
Thus, the angle formed by two vectors \(\vec u\) and \(\vec v\) of an orthonormal basis has (“principal”) measure \(\pi/2\) or \(-\pi/2\). When the principal measure of the angle \([(\vec u,\vec v)]\) is \(\pi/2\), we say that the basis is direct, when the principal measure is \(-\pi/2\), we say that the basis is indirect. More simply, an orthonormal basis \((\vec u,\vec v)\) is direct exactly when \(\vec v)\) is the image of \(\vec u)\) by the rotation of angle \(\pi/2\), which is the linear application \((x,y)\in\mathbb R^2\mapsto (-y,x)\). Thus, such a basis is direct exactly when \(\vec v=(-b,a)\) for \(\vec u=(a,b)\). In the same way, the orthonormal basis \((\vec u,\vec v)\) is indirect exactly when \(\vec v\) is the image of \(\vec u\) by the rotation \(-r\), of angle \(-\pi/2\), that is to say when \(\vec v=(b,-a)\) These two types of orthonormal bases correspond to two possible orientations of the Euclidean plane.
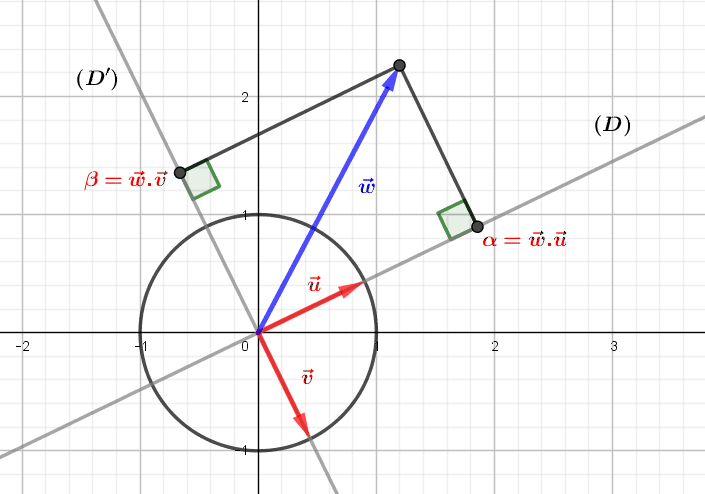
3.3. Decomposition in an orthonormal basis
An interest of orthonormal bases is to be able to obtain the decomposition of any vector directly from its scalar product with the vectors of the basis. Let \(B=(\vec u=(a,b),\vec v=(c,d))\) be an orthonormal basis and \(\vec w=(x,y)\) a plane vector. In this situation, the decomposition of \(w\) is simply \(\vec w=(\vec w.\vec u)\vec u+(\vec w.\vec v)\vec v\) (note that here the point denotes the scalar product). To demonstrate this, let us write \((\vec w.\vec u)\vec u+(\vec w.\vec v)\vec v=(ax+by,cx+dy)\vec u+(ax+by,cx+dy)\vec v\) \(=(a(ax+by)+c(cx+dy),b(ax+dy)+d(cx+dy))\). By the preceding paragraph, we have either \(\vec v=(-b,a)\), or \(\vec v=(b,-a)\): let us place ourselves in the first case, the other being analogous. The previous expression is simplified to \((a^2x+b^2x,b^2y+c^2y)\), or \((x,y)=\vec w\). Geometrically, the coefficients \(\vec w.\vec u\) and \(\vec w.\vec v\) are the respective “coordinates” of the orthogonal projections of \(\vec w\) on the directions of \(\vec u\) and \(\vec v\).

0 Comments