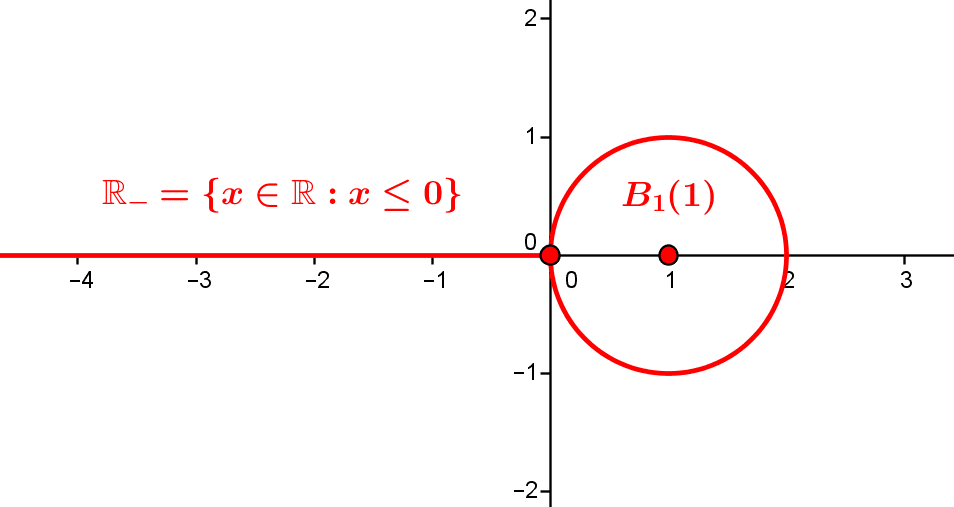
by Jean Barbet | May 8, 2021 | Algebra, Geometry, Non classé
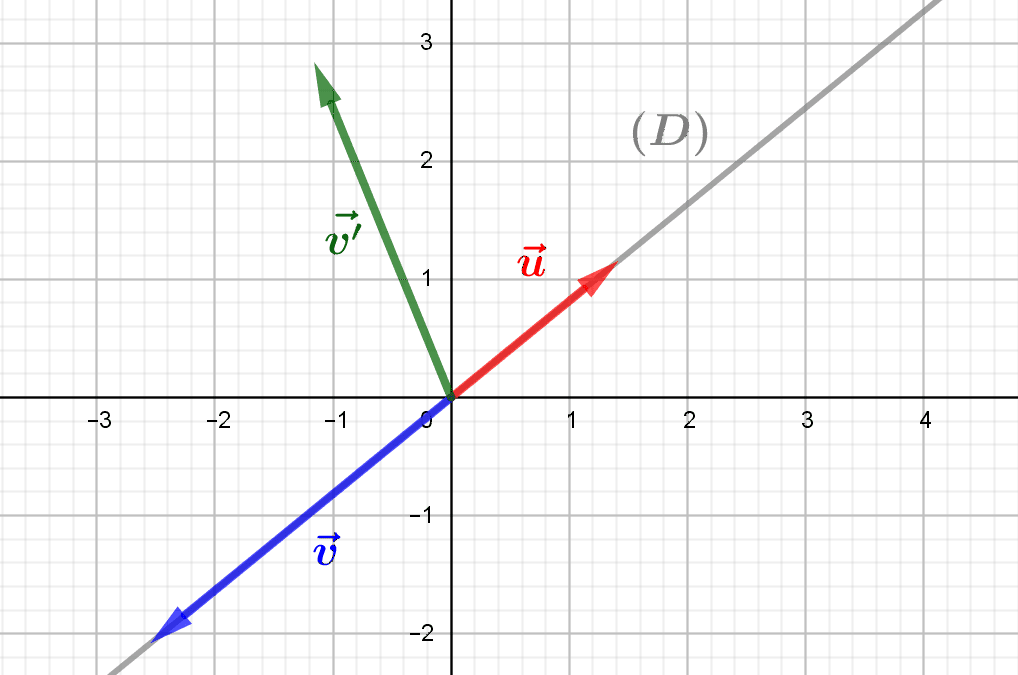
The representation of the Euclidean plane as the Cartesian product \(\mathbb R^2\) allows us to decompose any vector of the plane into two coordinates, its abscissa and its ordinate. This decomposition is linked to a particular and natural “representation...
by Jean Barbet | Mar 12, 2021 | Algebra, Non classé, Number Theory
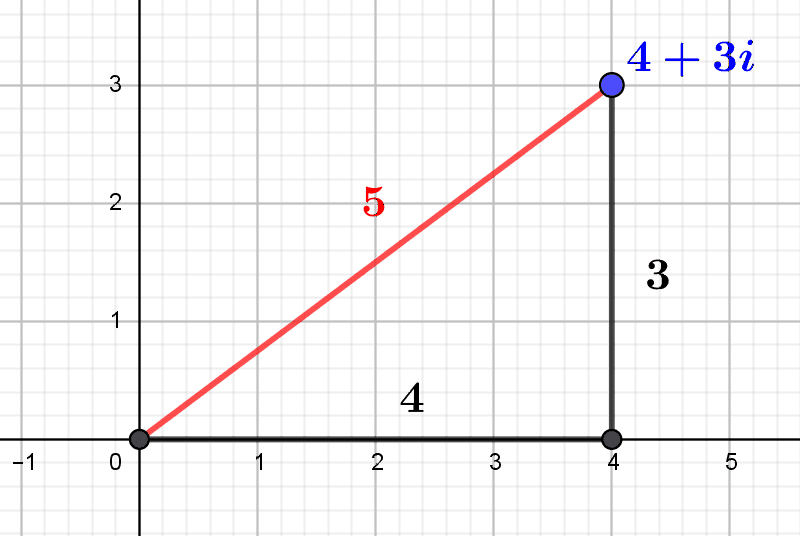
Gaussian integers are complex numbers with integer coordinates. Thanks to their norm, a kind of integer measure of their size, we can describe some of their arithmetic properties. In particular, we can determine which are the usual prime numbers that...
by Jean Barbet | Jan 9, 2021 | Analysis, Functions, Non classé
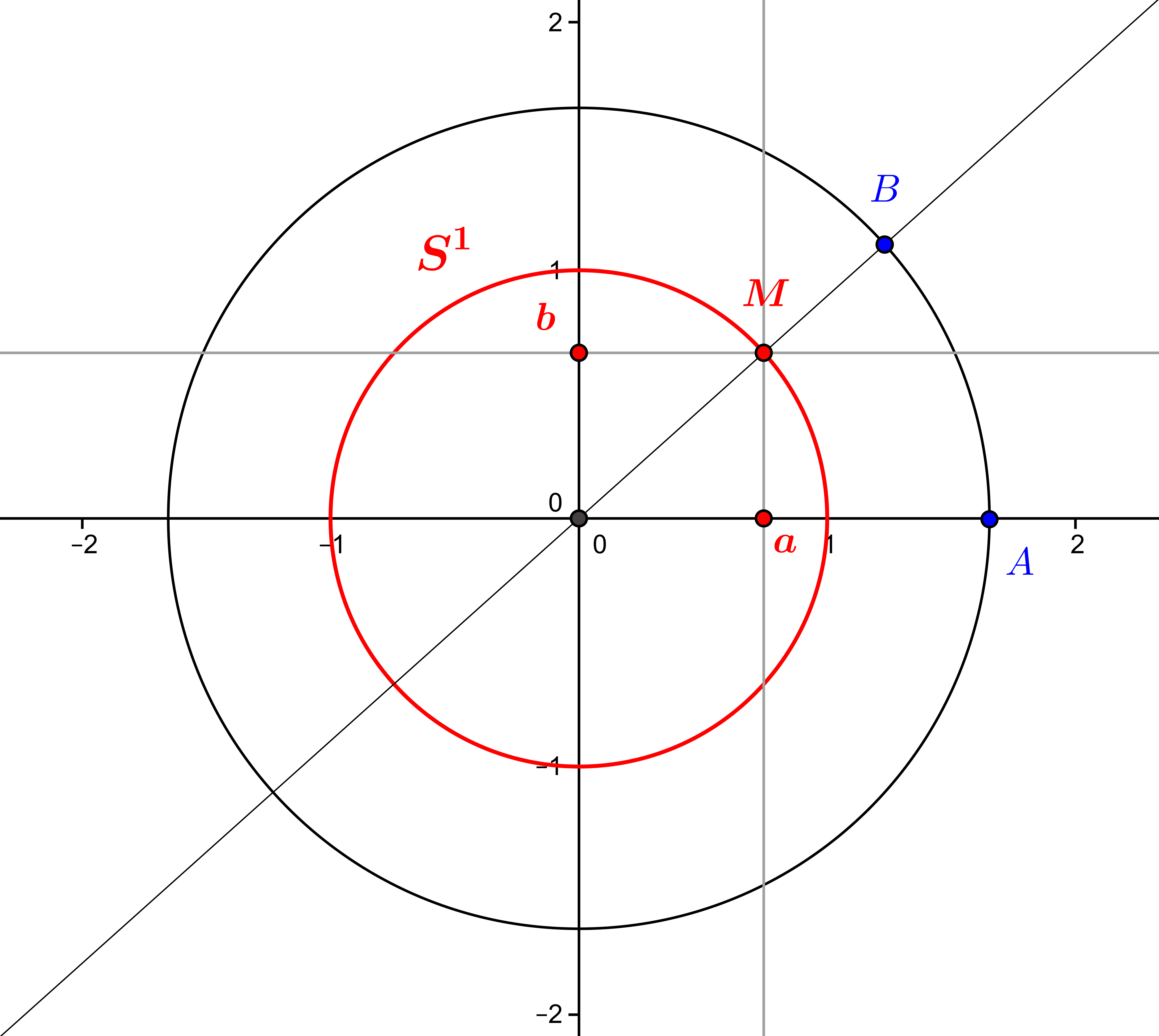
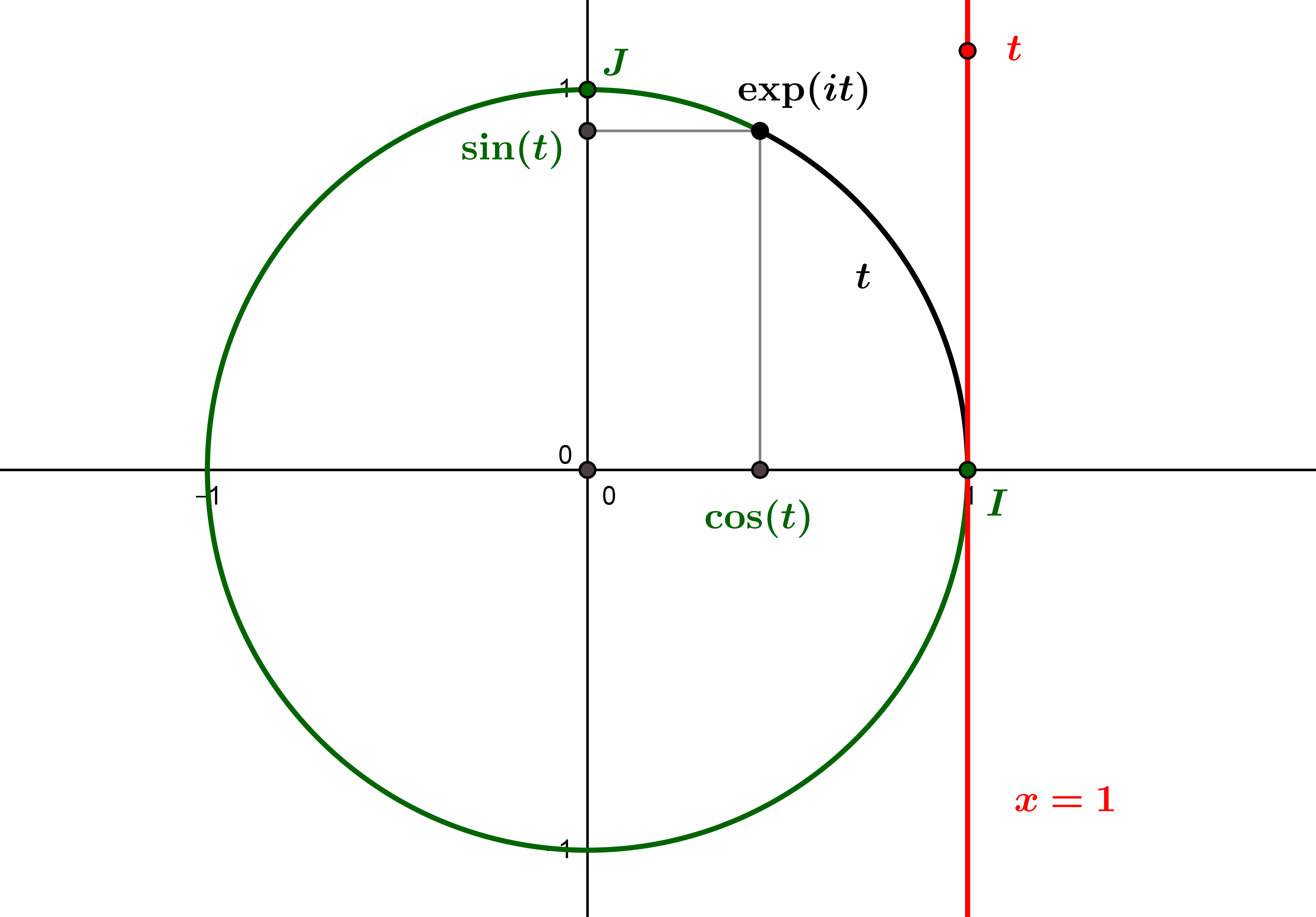
From the complex exponential function, we can define a “circular exponential” function, which “wraps” the real line around the trigonometric circle, and makes it possible to rigorously define the cosine and sine trigonometric functions, which...
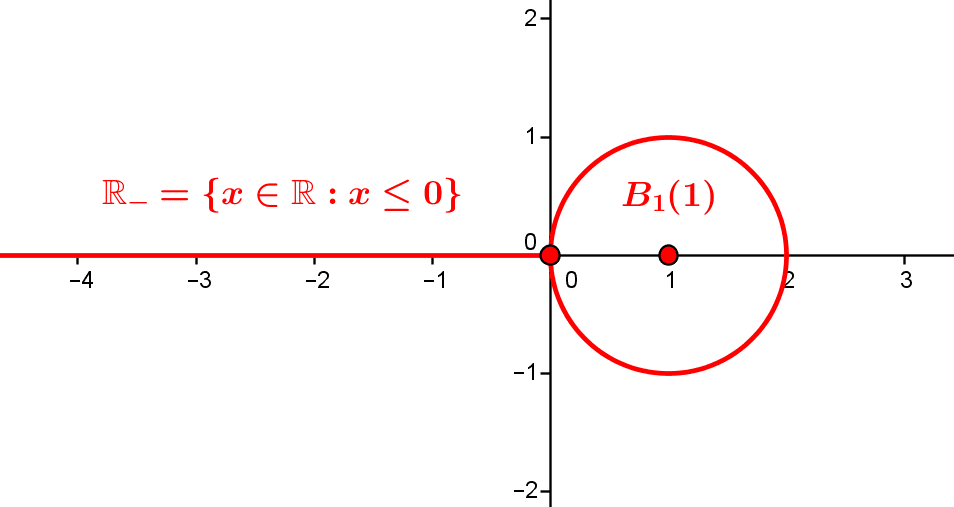
by Jean Barbet | Dec 29, 2020 | Analysis, Functions, Non classé
Some functions that can be differentiated indefinitely can be described ‘around each point’ as the sum of an power series. These are analytic functions, real or complex, the typical example being the exponential function, which can be extended to the whole complex...
by Jean Barbet | Dec 16, 2020 | Non classé, Number Theory, Set Theory
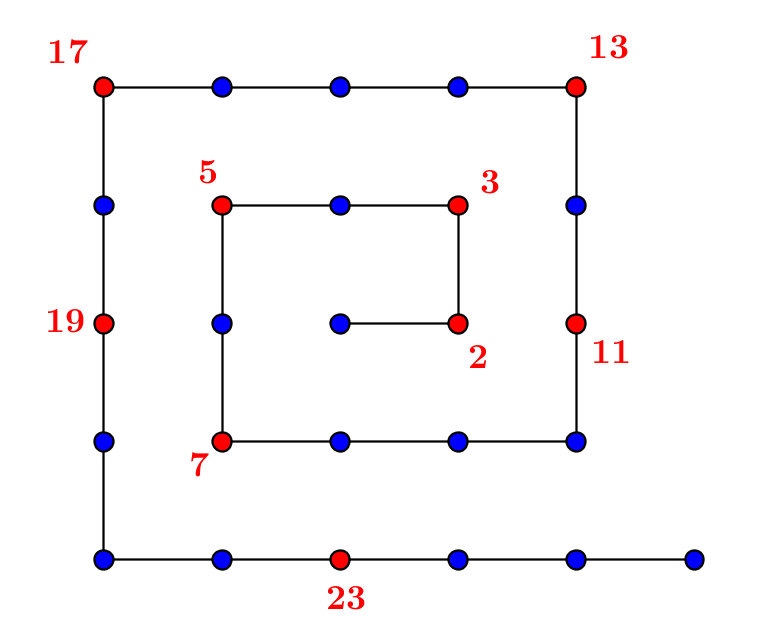
The prime natural numbers are those which have no divisors other than 1 and themselves. They exist in infinite number by Euclid’s theorem, which is not difficult to prove. 1.Prime numbers 1.1.Divisors and primes A prime number is a non-zero natural number (see...