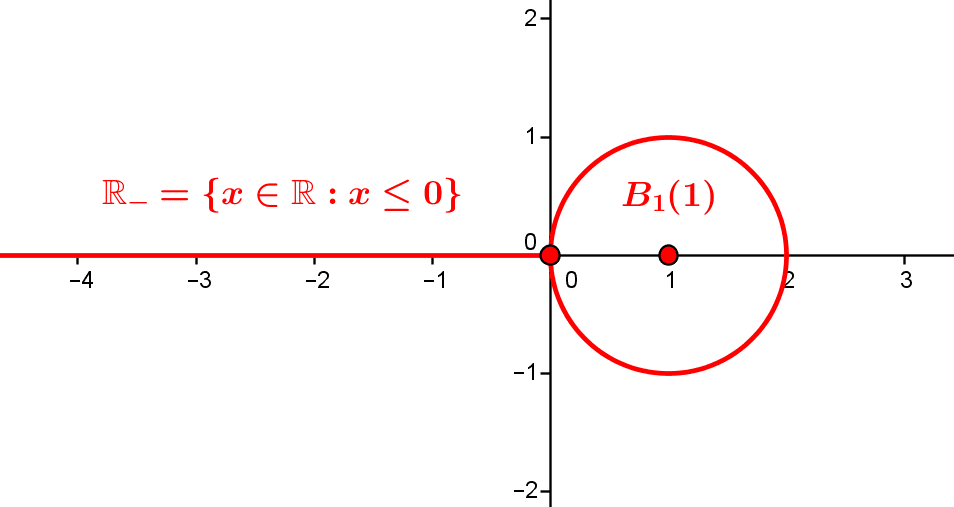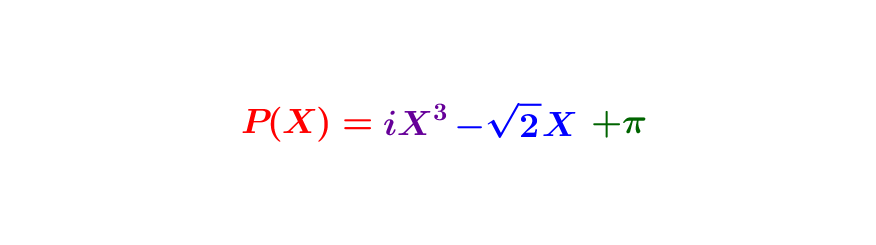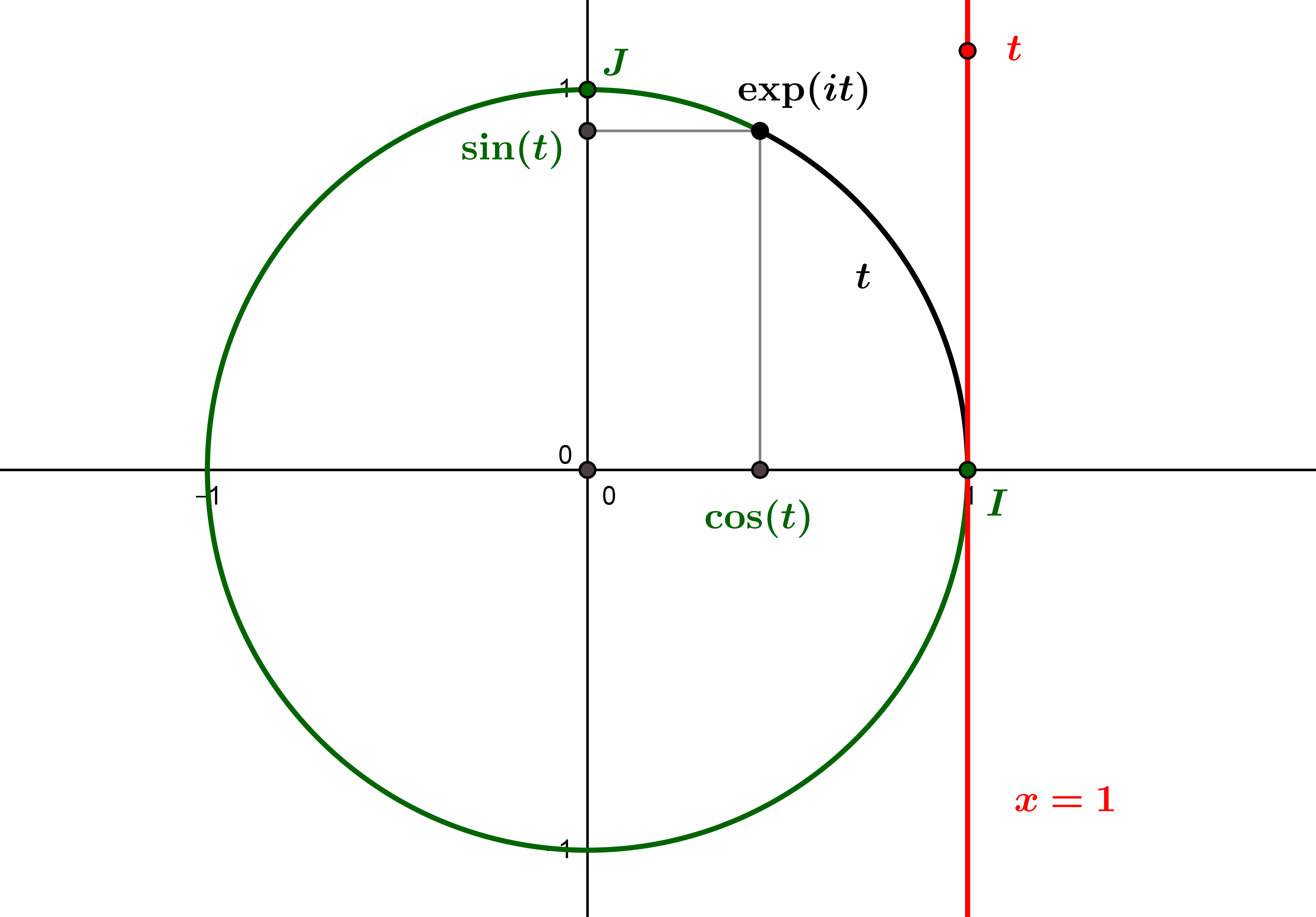
by Jean Barbet | Jan 9, 2021 | Analysis, Functions, Non classé
From the complex exponential function, we can define a “circular exponential” function, which “wraps” the real line around the trigonometric circle, and makes it possible to rigorously define the cosine and sine trigonometric functions, which...
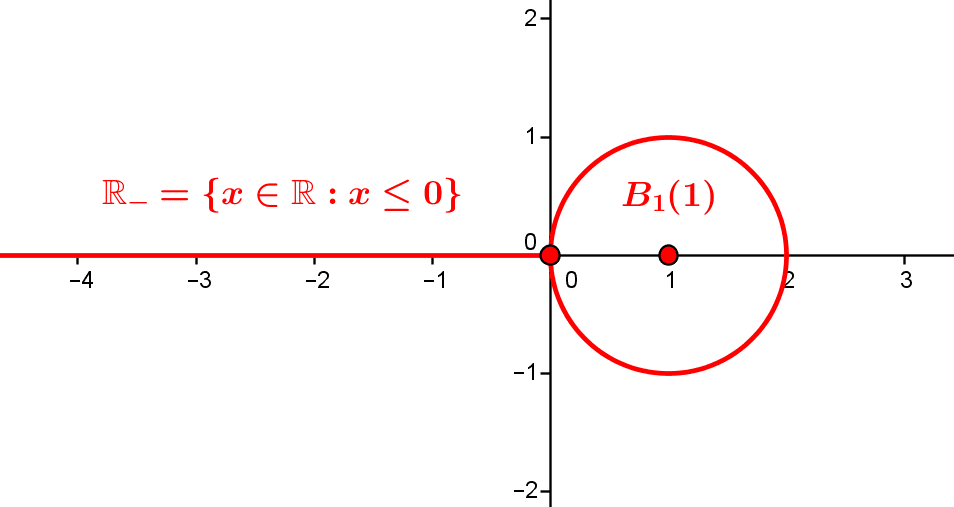
by Jean Barbet | Dec 29, 2020 | Analysis, Functions, Non classé
Some functions that can be differentiated indefinitely can be described ‘around each point’ as the sum of an power series. These are analytic functions, real or complex, the typical example being the exponential function, which can be extended to the whole complex...
by Jean Barbet | Dec 6, 2020 | Analysis, Functions
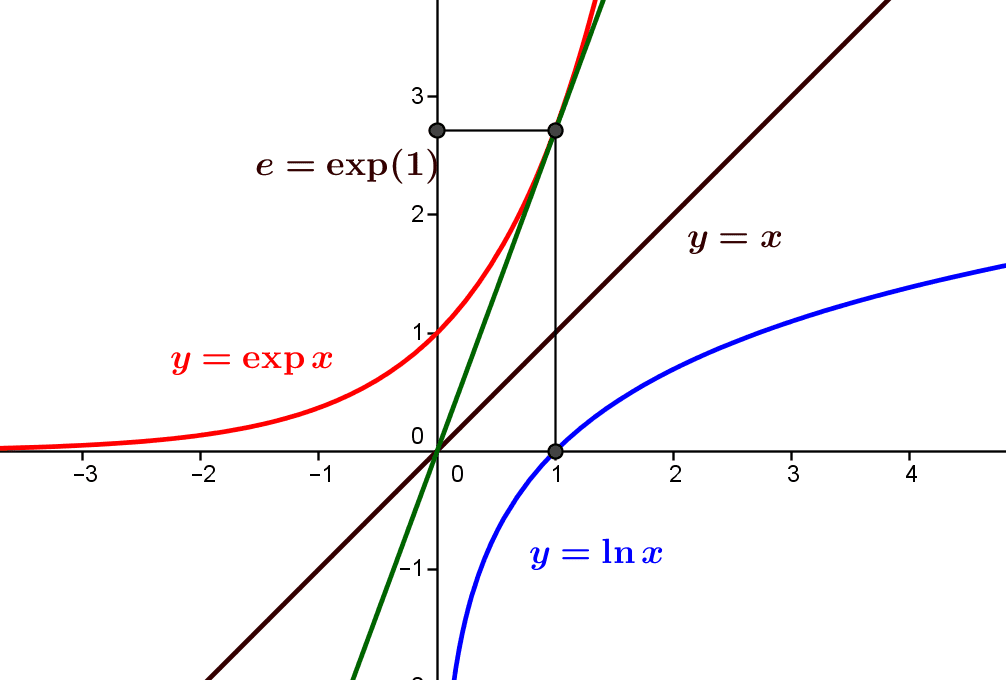
The relations between the properties of monotonicity, continuity and derivation of a function of one real variable allow us to formally derivate the inverse bijection of an injective and derivable function. The most representative example is perhaps that of the...
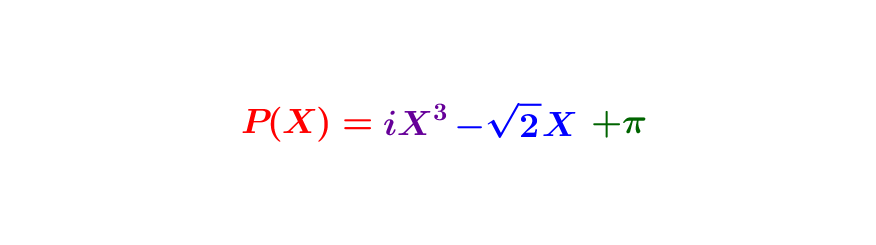
by Jean Barbet | Sep 16, 2020 | Algebra, Functions, Non classé
Polynomials with one variable are mathematical representations of the expressions used in polynomial equations. They allow algebraic methods to be applied to solving these equations. 1. Equations are “linguistic” objects 1.1 Polynomial equations and number...
by Jean Barbet | Jul 10, 2020 | Functions, Set Theory
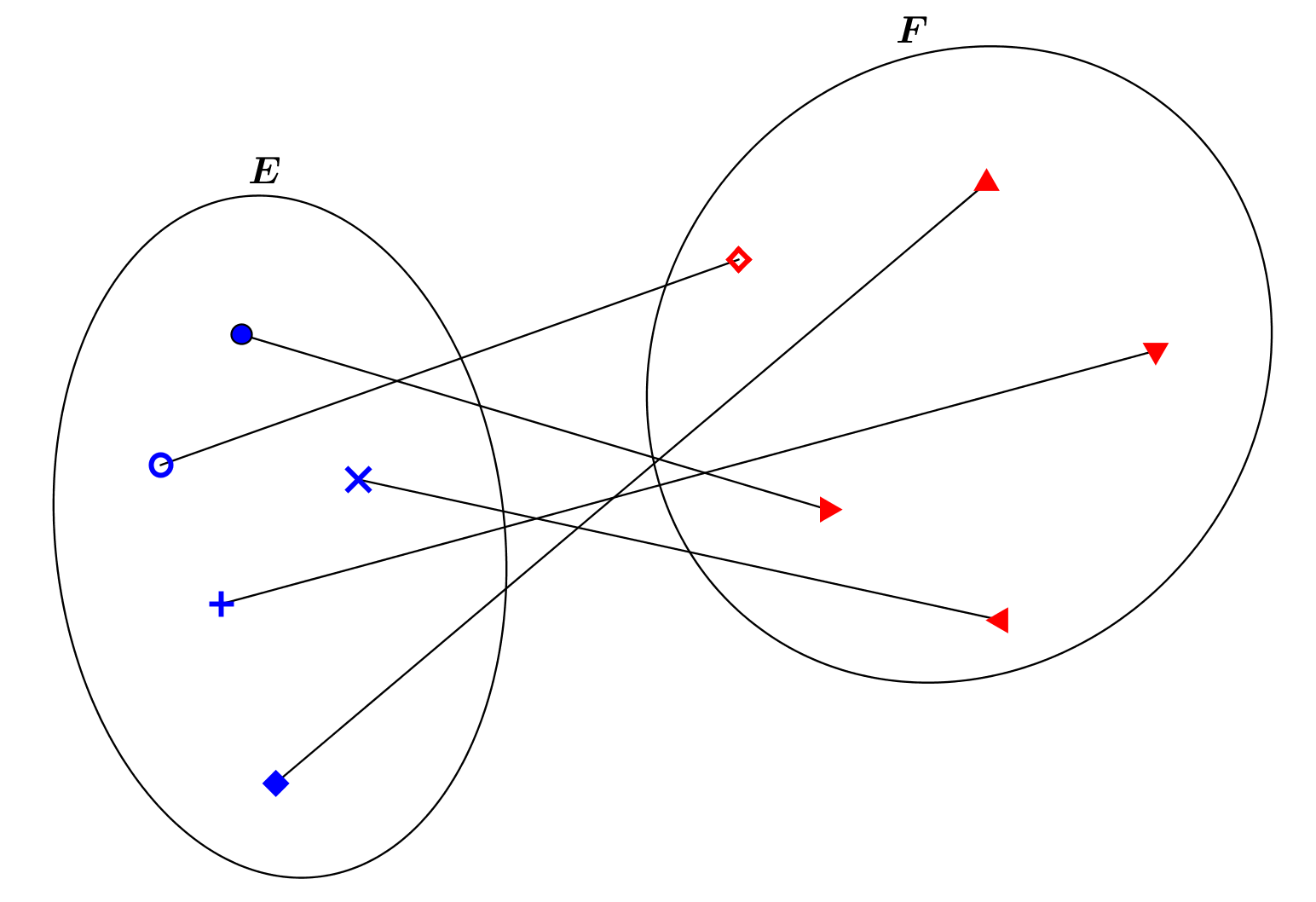
A finite set is a set that can be counted using the natural numbers \(1,\ldots,n\) for a certain natural number \(n\). But what is counting ? And then, what is an infinite set? 1.Comparing sets : the notion of bijection The notions of finite set and infinite set, and...

by Jean Barbet | Jul 6, 2020 | Functions, Geometry
The definition of a circle is simple: it is a set of points located at the same distance from a given point. This distance is called the radius and this point is called the centre of the circle. The circle with centre \((-1,-3/2)\) and radius \(\sqrt 6\) 1. Circles as...