Gaussian integers are complex numbers with integer coordinates. Thanks to their norm, a kind of integer measure of their size, we can describe some of their arithmetic properties. In particular, we can determine which are the usual prime numbers that “remain” prime as Gauss integers. We can also derive the “two square theorem”, which allows us to identify the natural numbers that may be written as a sum of two squares.
1. The ring of Gaussian integers
1.1. Complex numbers with integer coordinates
Gaussian integers are the complex numbers “with integer coordinates”, i.e. of the form $a+ib$, with $a$ and $b$ integers. The addition and multiplication of two Gaussian integers is a Gaussian integer, as shown by the formulae defining these operations on the complex numbers. Indeed, if $a+ib$ and $c+id$ are two such, we have $(a+ib)+(c+id)=(a+c)+i(b+d)$ and the numbers $a+c$ and $b+d$ are integers. Similarly, we have $(a+ib).(c+id)=(ac-bd)+i(ad+bc)$ and the numbers $ac-bd$ and $ad+bc$ are integers. Since $0=0+i0$ and $1=1+i0$ are Gaussian integers, they form a so-called subring of the field $\mathbb C$ of complex numbers, which is denoted $\mathbb Z[i]$. As such, this subring is an integral domain: if $z$ and $w$ are two Gaussian integers such that $z.w=0$, then $z=0$ or $w=0$; in other words, the product of two non-zero Gaussian integers is non-zero.
1.2. Norm and invertibility
The “size” of a Gaussian integer $z=a+ib$ is measured by its (arithmetic) norm, which is the natural number $N(z)=a^2+b^2$. This is in fact the product $z\times \overline z$, not to be confused with the Euclidean norm or module of $z$, which is the square root of $N(z)$. The norm is a multiplicative function $N:\mathbb Z[i]\to \mathbb N$. This means that for two Gaussian integers $z$ and $w$, we have $N(z.w)=N(z).N(w)$, which can be verified by calculation. From this we can deduce that a Gaussian integer $z$ is invertible if and only if its norm is invertible, i.e. is $1$. The only invertible Gaussian integers are $1$, $-1$, $i$ and $-i$, the inverse of $i$ being $-i$ since $i.(-i)=-i^2=1$. We can also derive valuable information about arithmetic in $\mathbb Z[i]$, as we shall see.

2. An imaginary Euclidean division
2.1. An analogy with Euclidean division of integers
Let us recall the classic Euclidean division: if $m, n$ are two integers and $n>0$, there exist two unique integers \(q\) (the quotient) and \(r\) (the remainder) such that$ m=q\times n +r$ and $0\leq r<n$. This expression is what is called the Euclidean division of $m$ by $n$. The restriction on $r$ is not necessary: one could choose a strictly negative $r$, and then there would always exist two integers $q$ and $r$ such that $m=q.n+r$ and $|r|<|n|$, although $q$ and $r$ are no longer unique in this version. However, by replacing the absolute value of the integers by the norm of Gaussian integers, we can define an analogous Euclidean division in \(\mathbb Z[i]\). One proceeds as follows: if \(z=a+ib\) and \(w=c+id\) are two Gaussian integers with \(w\neq 0\), one divides \(z\) by \(w\) in \(\mathbb C\) : we obtain \[z/w=z\overline w/w\overline w=\frac{(ac-bd)+i(ad+bc)}{c^2+d^2}= x+iy\] with \(x, y\) rational numbers. We then choose two integers \(m,n\) such that \(|x-m|\leq 1/2\) and \(|y-n|\leq 1/2\) : by putting \(q=m+in\) and \(r=z-q.w\), we have two Gaussian integers and by the properties of the norm we can then write \(z=q.w+r\), with \(N(r)<N(w)\) ! We can thus state
Theorem 1
If \(z\) and \(w\) are two Gauss integers and \(w\neq 0\), then there exist two Gauss integers \(q\) and \(r\) such that \(z=w.q+r\) and \(N(r)<N(w)\).
2.2. Examples of divisions in \(\mathbb Z[i]\)
Let us carry out a Euclidean division of \(z=8+3i\) by \(w=-2-5i\): first we find \(z/w=(-31/29)+i(34/29)\), so we can only choose \(m=-1\) and \(n=1\), and we get \(q=-1+i\), hence \(r=z-qw=(8+3i)-(7+3i)=1\), and therefore we have \(8+3i=(-1+i). (-2-5i)+1\). We see that we have \(N(r)=1<29=N(w)\). In this example, only one choice for \(q\), and thus for \(r\), is possible, but if we divide this time \(z=4+17i\) by \(w=4+2i\), we obtain \(z/w=(5/2)+3i\), so we can choose either \(m=2i\) – and then we have \(q=2+3i\) and \(r=2+i\) – or \(m=3i\) – and then we have \(q=3+3i\) and \(r=-2-i\) – and both solutions fit! This is what already happens with the Euclidean division of the integers: dividing $14$ by $3$, the standard division gives $14=4.3+2$ (i.e. $q=4$ and $r=2$), but we also have $14=5.3-1$ (i.e. $q=5$ and $r=-1$). The preferred choice is then the one where the remainder is positive; by analogy, we can fix a preferred choice of Euclidean division in $\mathbb Z[i]$ by imposing when necessary, to choose for $m$ or $n$ the respective integer parts of $x$ or $y$ in the previous section.
3. Not so prime numbers
3.1. Prime Gaussian integers
In the set of natural numbers, a number $p$ is said to be prime if it is divisible only by $1$ and by itself (see An infinite number of primes). We can say that an integer $p$ is prime if $|p|$ (its absolute value) is a prime number. This means that $p$ is divisible only by $1$, $-1$, $-p$ and itself, i.e. it is divisible only by an invertible element ($1$ or $-1$) of $\mathbb Z$ or by the product of $p$ by an invertible element ($p$ or $-p$). We have a corresponding notion in the ring $\mathbb Z[i]$ : a Gaussian integer $z=a+ib$ is said to be prime (or irreducible, equivalent notion in this case) if its only divisors are the invertible elements of $\mathbb Z[i]$ (either $1$, $-1$, $i$ or $-i$), and the products of $z$ by an invertible element (either $z$, $-z=-a-ib$, $iz=-b+ia$ or $-iz=b-ia$).
3.2. Prime natural numbers and sums of two squares
However, some primes in $\mathbb Z$ are no longer prime when considered as members of $\mathbb Z[i]$! For example, in $\mathbb Z[i]$ we have $(1+i).(1-i)=1^2-i^2=1+1=2$, and as this also shows that $N(1+i)=N(1-i)=2$, the Gaussian integers $1+i$ and $1-i$ are not invertible. Thus, the number $2$ is no longer prime as a Gaussian integer! The existence of the decomposition here comes from the fact that $2$ is the norm of a non-invertible Gaussian integer, and therefore also of its conjugate. In general, a positive prime $p$ is the norm of a Gaussian integer exactly when it is the sum of two squares. Now, it can be shown that this is equivalent to $p\equiv 1\ [4]$, i.e. $p-1$ is a multiple of $4$. In this case, the number $p=a^2+b^2$ cannot be prime in $\mathbb Z[i]$, since $p=N(a+ib)>1$.
4. The two square theorem
4.1. Remaining prime in $\mathbb Z[i]$
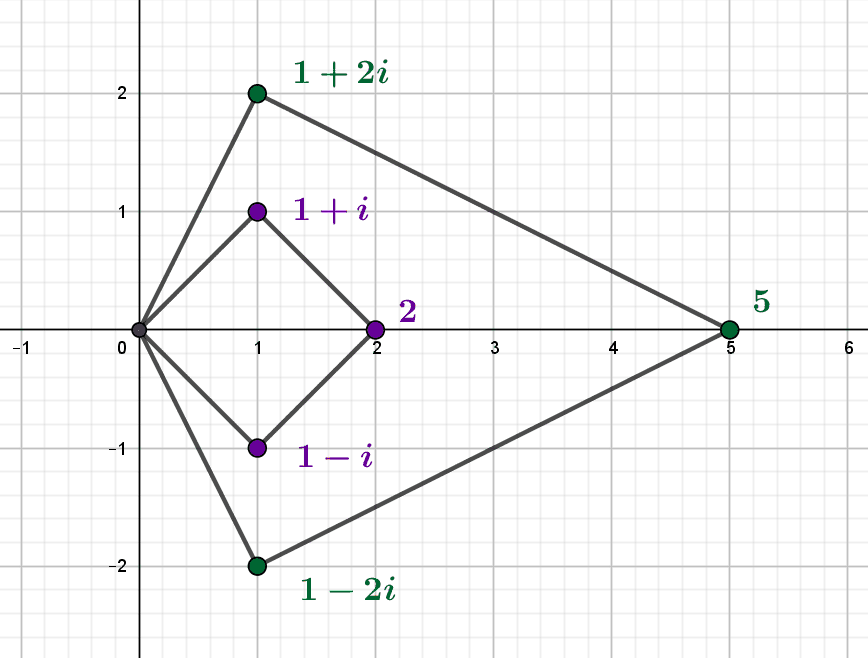
This criterion allows in fact to determine exactly which prime numbers $p$ remain prime in $\mathbb Z[i]$. Indeed, if $p$ is the sum of two squares, it cannot be prime in $\mathbb Z[i]$ in general. Conversely, if $p$ is not prime in $\mathbb Z[i]$ it can be decomposed into the form $p=z.w$ with $z$ and $w$ non invertible. This means that $N(z),N(w)\neq 1$, so we have $p^2=N(p)=N(z).N(w)$ in $\mathbb N$, and since $p$ is prime, $N(z)=p$ or $N(z)=-p$, so $|p|$ is the sum of two squares. Combining this with the previous paragraph, we see that since $5-1=4$, $5$ is not prime in $\mathbb Z[i]$ – and indeed we have $5=1^2+2^2=(1+2i).(1-2i)$ – whereas $3$ is prime in $\mathbb Z[i]$ since $3-1=2$ is not a multiple of $4$.
4.2. The two square theorem
Thus, a prime natural number $p$ is not a Gaussian prime if and only if it is the sum of two squares of integers, if and only if $p=2$ or $p\equiv 1\ [4]$. Using the decomposition of integers into products of prime factors, we can then prove the two square theorem. This theorem allows us to determine which natural numbers $>0$ are the sum of two squares of integers, i.e. the norm of a Gaussian integer. These are exactly the numbers $n$ whose prime factors $p$ congruent to $3$ modulo $4$ (i.e. such that $p-3$ is a multiple of $4$), appear with an even exponent. We can also say when the decomposition into two squares is unique: namely when $n$ has only one prime factor $p$ congruent to $1$ modulo $4$ and it appears with exponent $1$.
Conclusion
Calculating with Gaussian integers is not just a fancy way of showing off mathematical curiosities. It is also a way to better understand the nature of the usual prime numbers, thanks to the “higher” reality of the complex numbers. “Imaginary” arithmetic thus allows us to better probe the properties of the natural numbers, here in the form of a theorem that does not even mention the Gaussian integers.

0 Comments