Integers are an extension of the natural numbers where the existence of subtraction provides a more appropriate framework for certain questions of arithmetic. They can be described axiomatically, but can also be constructed from the set of natural numbers and some naive set theory.
1.The intuition of integers
The integers \(\ldots,-3,-2,-1,0,1,2,3,\ldots\) form an intuitive set \(\mathbb Z\), which is an extension of the set \(\mathbb N\) of natural numbers (see What is a natural number?). To these we have added opposites for addition, i.e., for any natural number \(n\), an integer \(-n\) such that \(n+(-n)=0\). Any integer has therefore an opposite \(-n\) for the addition, and this makes it possible to define a new operation, the subtraction of any two integers \(a\) and \(b\), by posing \(a-b=a+(-b)\).
In the set \(\mathbb Z\) one can extend the usual operations \(+\) and \(\times\) between the natural numbers, as well as the relation \(<\) of strict order which allows to compare them. The main elementary interest of the set \(\mathbb Z\) is that the relations between addition and multiplication extend to it and develop into relations between subtraction and multiplication. For example, the distributivity of the multiplication on the addition is still valid there: if \(m, n, p\) are three integers, we always have the equality \(m\times (n+p)=m\times n+m\times p\).
Now thanks to the existence of the subtraction, one can then simplify the demonstration of theorems of arithmetic, like the one which makes it possible to define the Euclidean division. It is also a more natural framework for the expression of some of these theorems, like Bézout’s theorem: if \(m\) and \(n\) are two integers with greatest common divisor \(d\), then there exist two integers \(u,v\) such that \(au+bv=d\).

Graphical representation of a few integers
2.Rather construct the integers
In mathematics, we like to do without too many first principles (axioms, postulates), and rather than admitting the “existence” of such a set \(\mathbb Z\) with these properties, we prefer alternatively to build it. Such a “construction” is a first example of the definition of a number system from a simpler system, here the set \(\mathbb N\) of natural numbers. Thanks to naive set theory (see What is a set?), we can thus base the description of the set \(\mathbb Z\) on the sole axioms describing the set \(\mathbb N\).
The idea underlying such a construction or representation of the integers is to consider them as operations on the natural numbers. Such an operation is then conceptualised by a pair \((a,b)\) of natural numbers, which represents “what to add” to obtain \(b\) from \(a\). In other words, the couple \((a,b)\) represents the “subtraction” \(b-a\) in the set \(\mathbb Z\) that we want to describe. The order is important : the couple \((b,a)\) is different from the couple \((a,b)\), and represents of course another operation, namely \(a-b\) !
3.A natural extension of the set \(\mathbb N\)
Thanks to this representation, one can already consider any natural number \(n\) as an “operation”, namely \(0,n)\), since \(n-0\) must correspond to \(n\) in the set \(\mathbb Z\). It should be noted here that if \(a\) is any natural number, the operation \((a,a+n)\) also represents the natural number \(n\)! The interest of the construction appears however when one chooses \(a,b\in\mathbb N\) such as \(a>b\), because then the couple \((a,b)\) does not represent any natural number \(n\), since there is no such number such that \(b-a=n\), because \(b-a\) would be strictly negative ! This also means that for any natural number \(n\), we can represent the opposite “\(-n\)” of \(n\) as the pair \((n,0)\).
But be careful: as we have noted, several pairs represent the same operation between two natural numbers, and therefore the same integer. Indeed, any pair \((a,b)\) represents the same operation (namely \((b-a)\)) as the pair \((a+n,b+n)\), for \(n\) any natural number, since \((b+n)-(a+n)=b+n-a-n=b-a\). This means that it is not the set of pairs \((a,b)\) of natural numbers which must represent the set \(\mathbb Z\) of integers. In fact, we say that two couples \((a,b)\) and \((c,d)\) are equivalent if they represent the same intuitive integer, and this amounts to saying that \(b-a=d-c\), in other words that \(a+d=b+c\). An integer is therefore a set of pairs \((a,b)\) of equivalent natural numbers, which we note \([(a,b)]\). Thus, if \((a,b)\) and \((c,d)\) are equivalent, we have \([(a,b)]=[(c,d)]\), and vice versa!
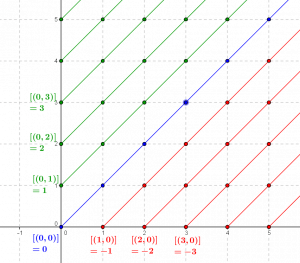
Representation of the integers constructed as “sets of pairs of equivalent natural numbers” (the pairs of natural numbers are represented as nodes of the plane with integer coordinates). Each half-line represents an integer by connecting pairs that represent the same integer. The red half-lines represent strictly negative integers, the blue half-line represents zero, and the green half-lines represent strictly positive integers
4.The extension of \(+\), \(\times\) and \(<\) to the integers
If we now consider the set \(\mathbb Z\) as the set of these “equivalence classes” of pairs of natural numbers, we can extend the addition of the natural numbers by \([(a,b)]+[(c,d)]=[(a+c,b+d)]\) and their multiplication by \([(a,b)]\times [(c,d)]=[(bd+ac,ad+bc)]\). One can also extend the order \(<\) between natural numbers by decreeing that \([(a,b)]<[(c,d)]\) if and only if \(a+d<b+c\).
In this way, the usual elementary properties of \(+\), \(\times\) and \(<\) extend from the set \(\mathbb N\) to the set \(\mathbb Z\) as newly constructed. And we notice, this is the purpose of the construction, that any integer \([(a,b)]\) now has an opposite for addition, namely \([(b,a)]\), since by definition, we have the equality \([(a,b)]+[(b,a)]=[(a+b,a+b)]=[0,0]\), and that \([(0,0)]\) is evidently the “zero” of addition. One could demonstrate all the intuitive properties of \( \mathbb Z\) from these definitions.
Once we have understood this construction, for \(n\) a natural number we can still write \(n\) the integer \([(0,n)]\), and \(-n\) the integer \([(n,0)]\), then forget everything we have just done, to use the integers as we are used to ! Only, we now know that the set \(\mathbb Z\) of integers can be described from the o

0 Comments