From Descartes’ analytic approach, which consists in introducing coordinates to represent the points of the plane, and from Cauchy’s construction of the real numbers, we can give a modern representation of the euclidean plane from which we recover Euclid’s geometric axioms.
1. The synthetic approach of Euclid (and Hilbert)
1.1.Euclid’s geometry of the plane
The Greek mathematician Euclid is famous for his postulates and axioms of plane geometry, concerning lines, segments, circles, angles, parallelism, perpendicularity… and to this day, they are used for the geometry of these objects in the plane, and precisely called Euclidean (plane) geometry. This approach is what is known in mathematics as a synthetic approach: from axioms, which are a formulation of the intuition of elementary properties of mathematical objects, one establishes properties thanks to deductions (demonstrations), involving no calculation.
1.2.Hilbert’s completion and the question of calculus
The Euclidean approach, which has been valid since Antiquity, nevertheless has certain limitations. On the one hand, there is a “lack of axioms” to prove all of Euclid’s theorems (some demonstrations implicitly referred to unestablished properties), which the German mathematician David Hilbert, among others, remedied in 1899 by proposing a more complete list of axioms. On the other hand, in ancient Greek mathematics, calculations of “areas”, as in the Pythagorean theorem, are in fact statements about recompositions of geometric figures: the synthetic approach is not articulated to the calculation, which is lacking in its interpretation in modern mathematics.
2. The analytical approach of Descartes: coordinates and calculation
2.1.Descartes’ analytical method : the coordinates
In modern times, the French mathematician and philosopher René Descartes invented the “coordinates” of a point in the plane: such a point \(M\) can be represented by a pair \((x,y)\) of numbers, \(x\) being the abscissa and \(y\) being the ordinate of the point \(M\). These coordinates correspond to the projections of the point \(M\), perpendicularly, on two “axes”.
This makes it possible to introduce calculus into plane geometry, since one can then, for example, represent lines by equations; the intersection of two non-parallel lines is a point, whose co-ordinates can be determined by “analytical”, i.e. in this case calculative, procedures, from equations of the two lines or numerical parameters which describe them.
2.2.Incommensurable geometric quantities : enter the real numbers
However, if this method is well adapted to what is called “affine geometry” (the part of geometry that deals with lines and parallelism in this context), at the time rational numbers were not sufficient to deal with certain quantities linked in particular to triangles and circles. Indeed, according to Pythagoras’ theorem, if we want to assign a measure of length to the diagonal of a right-angled triangle, it must be a square root of the sum of the squares of the lengths of the other two sides.
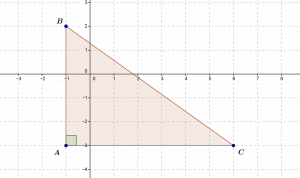
In the triangle \(ABC\), rectangular at \(A\), by Pythagoras’ theorem the area of the square constructed on the hypotenuse (i.e. the segment \([BC]\)) is the sum of the areas of the squares constructed on the sides \([AB]\) and \([BC]\). Thus, the square \(BC^2\) of the length \(BC\) of the side \([BC]\) should be equal to the sum \(AB^2+AC^2\), or in this case \(5^2+7^2=25+49=74\), or \(BC=\sqrt{74}\).
Now, when lengths are measured by rational numbers in the ancient tradition, such a square root does not always exist. For example, the diagonal of a square of length \(1\) must be a number whose square is \(2\), and it can be shown that this number does not exist, which was known in ancient times and was a real Greek tragedy… It is said that “the diagonal of the unit square is incommensurable”. For the analytical approach to be useful for all Euclidean geometry, it must therefore be applicable to all its objects, and in particular angles and circles. It is thanks to the construction of the real numbers that the possibility of doing so has been put on a firm basis.
3. Representing the Euclidean plane using the set of real numbers
3.1.The real numbers beyond the traditional limitations
The construction of real numbers (see the article What is a real number ?) made it possible to solve the problem of the “existence” of certain quantities which it was not possible to find in the set of rational numbers, such as certain solutions of numerical equations (known as Diophantine), and in particular the existence of square roots for all positive numbers.
In particular, as regards the translation in or by the calculation of the properties of Euclidean geometry, the limits of the Cartesian approach by coordinates associated with the calculation of lengths, are lifted if one wants to conceive that the coordinates of a point of the plane are real numbers and not rational numbers. In other words, the “Pythagorean” tragedy of the incommensurability of the diagonal of the unit square found a happy ending in modern times, but Greek civilisation did not benefit from it (as far as we know).
3.2.\(\mathbb R^2\) as a set-theoretic representation of the Euclidean plane
But today we can interpret this application of the theory of real numbers to Euclidean geometry as the possible refoundation of this ancient geometry on modern, “analytical” bases. Indeed, from the Cartesian idea that one can represent a point of the plane from its coordinates, which are henceforth a couple of real numbers, one can in fact define a point of the plane as such a couple of real numbers !
Thus, we can state that the “Euclidean plane” is the set of pairs \((x,y)\) of real numbers, and the resources of naive set theory (see the article What is a set ?) allow us to give a perfectly clear description of it as the Cartesian product (an adjective taken from “Descartes”) of the set \(\mathbb R\) of real numbers by itself, that is to say the set noted \(\mathbb R\times\mathbb R\) or \(\mathbb R^2\). This way of doing things is well adapted to modern mathematical rigour, which is based on set theory, and integrates both the calculatory approach by coordinates, and the synthetic approach by axioms. Indeed, it can be shown that all the axioms of Euclid (and Hilbert) are “true” in the plane \(\mathbb R^2\), if at least we “interpret” the lines, points, segments, circles, angles, parallelism, perpendicularity… in this new language, which is the object of linear algebra and Euclidean affine geometry. We have found what we call a model of Euclidean geometry.
3.3.The Euclidean distance in modern plane geometry
One of the key elements of this interpretation is the notion of Euclidean distance: inspired by Pythagoras’ theorem, we can consider that the distance between two points \(A=(a_1,a_2)\) and \(B=(b_1,b_2)\) is the length of the hypotenuse of the right-angled triangle “defined” by these two points, and is thus defined as the real number whose square is \((b_1-a_1)^2+(b_2-a_2)^2\), i.e. \[\sqrt{(b_1-a_1)^2+(b_2-a_2)^2},\] since \(|b_1-a_1|\) and \(|b_2-a_2|\) are the lengths of the sides of the triangle, as in the following figure (the sign |. | is the absolute value: the absolute value \(|x|\) of a number \(x\) is the one of the numbers \(x\) or \(-x\) that is positive, and \(x^2=|x|^2\) for any real \(x\)).

It should be noted that the Euclidean plane \(\mathbb R^2\) is the “basic structure” for the definition of the set \(\mathbb C\) of complex numbers: a complex number is nothing more, from this point of view, than a point of the Euclidean plane, considered “equipped” with a particular algebraic and geometric structure. But this is another story.
4. Beyond Euclid and Pythagoras: differential geometry
4.1.The fertility of the analytical representation
If the solution to the problem of the analytical description of Euclidean geometry appeared in the modern era and could be formalised thanks to the construction of real numbers, it is not by chance. This construction was part of a period of scientific and technical development in which functions were being studied and in which, with modern science, infinitesimal procedures (continuity, derivation, etc.) were being investigated.
Now, the introduction of the description of the Euclidean plane as \(\mathbb R^2\) has much more advanced consequences than Euclidean geometry. Whereas the latter only deals with lines, points, circles… which corresponded to the scientific and technical preoccupations of Antiquity, the analytic method now makes it possible to deal with differential geometry, i.e. with all forms and movements, having a certain regularity, in the plane, the space and in higher dimensions.
4.2.Back to the synthetic method in higher mathematics
It is therefore very curious in this respect that a recent mathematical discipline, synthetic differential geometry, allows us to reconstruct all of differential geometry – and potentially its applications to modern physics – from an approach that goes “backwards” to Euclid’s approach, i.e. with the help of axioms, upstream of any form of calculation. This is perhaps an expression of the unique timelessness of mathematical science.




0 Comments