A finite set is a set that can be counted using the natural numbers \(1,\ldots,n\) for a certain natural number \(n\). But what is counting ? And then, what is an infinite set?
1.Comparing sets : the notion of bijection
The notions of finite set and infinite set, and the mathematical conceptualisation of the “counting” (of the elements) of a set, are intimately linked and make it possible to distinguish and rigorously define the mathematical finite and infinite, without any other conceptual resource than naive set theory (see What is a set?).
In order to count the elements of a set (we say “enumerate”), we use the notion of bijection. A bijection between two sets \(E\) and \(F\) is a function (we also say an application, or a mappring) from \(E\) into \(F\), that is to say a “process” or an “operation” that transforms the elements of \(E\) into elements of \(F\) (mathematically we say that \(f\) associates to each element \(x\) of \(E\) an element \(y\), noted \(f(x)\), of \(F\)). This association is very peculiar : \(f\) is a bijection precisely when each element of \(F\) is associated by \(f\) to at most one element of \(E\) (we say we have an injective function) and that any element of \(F\) is associated to at least one element of \(E\) (we say we have an surjective function).
In other words, a function \(f:E\to F\) is a bijection exactly when it matches, one to one, the elements of \(E\) and of \(F\) ! One must thus often translate very simple ideas in a somewhat roundabout way to give them a certain mathematical rigour. But this way of pairing one by one the elements of two sets is in fact a natural way of comparing their quantities, even before counting them: children often proceed in this way!
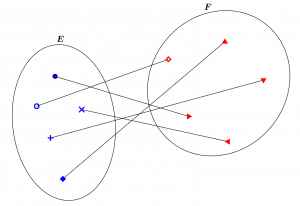
This figure illustrates the existence of a bijection between the sets \(E\) and \(F\): the elements of one and the other have been matched ” one to one”, so we can say that they have the “same number of elements”, without having to count them. There are several ways of establishing such a correspondence, and they can be counted precisely.
2.Finite sets are those that can be counted
By using this elementary but fundamental notion of bijection, we can rigorously define what a finite set is. A finite set is a set whose elements can theoretically be counted (enumerated), in other words a set which is in bijection with a set of the form \(1,2,3,\ldots,n\) (i.e. all the integers from \(1\) to \(n\) for a certain natural number \(n\)) . This simple definition conceptualises precisely the way we count: whereas we can compare two sets by putting them in bijection, we count a set by associating to each of its elements one and only one integer between \(1\) and the “number of elements” of this set (which is \(0\) if the set is empty…)! Mathematically, comparing two sets or counting a set is therefore the same thing, i.e. describing a bijection; only, when we count, we describe a bijection with a particular set, a set of numbers.
The set of numbers from \(1\) to \(n\) is noted \([[1,n]]\). To a finite set \(E\), we can thus attach a number of elements, which is the natural number \(n\) that we obtain by putting, by definition, \(E\) in bijection with the set \([[1,n]]\). Experience shows us that whatever the way we count, we end up with the same result; but is it theoretically true, in other words is it impossible to count a finite set in two different ways and obtain two different results? Even if it seems strange to ask this question, it is not part of the definition, and mathematical rigour demands that it be proved! It is indeed a theorem, which requires some thought. And the question is far from trivial, since when we enumerate an infinite set, at least using what we call an “ordinal” number, we can end up with different results…
Returning to finite sets, since any way of counting a set \(E\) – that is, conceptually, any bijection between \(E\) and a set of the form \([[1,n]]\) – gives the same result, one can define the number of elements of \(E\) as that single natural number \(n\), which is also called the cardinal of \(E\) (and in the case that the cardinal of an infinite set can be defined, it does not depend on the way of counting either). Some other “obvious” properties of finite sets need to be established rigorously, i.e. demonstrated: for example, that a subset \(S\) of a finite set \(E\) is itself finite, and that it has fewer elements than \(E\) ! In the same way, it is necessary to show that the union of two finite sets is a finite set…
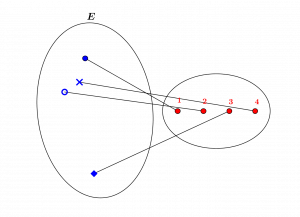
We enumerate the set \(E\) using the same principle of bijection: we associate one to one the elements of \(E\) with the first natural numbers, until we have associated all its elements: the set \(E\) is in bijection with the set \(\{1,2,3,4\}\), it thus has \(4\) elements.
3.The first of the infinite sets
This being said, since we have a rigorous mathematical definition of what a finite set is, in good logic we can define an infinite set as the “complementary” notion: an infinite set is a set which is not finite. This definition, the simplest possible, is disappointing for those who want to understand a little about mathematical infinity. It is nonetheless perfectly rigorous, in view of the definitions introduced so far, and it can be rephrased directly as follows: an infinite set is a set that cannot be counted, i.e. that cannot be put in bijection with a set of the form \([[1,n]]\). We have already made a progress in the understanding of the infinite: it “exceeds” everything that is finite. From here, we will give two more interesting characterisations of infinity.
To characterise a property is to establish that it is equivalent to another property, which can often serve as an alternative definition. The first of these characterisations is linked to the set \(\mathbb N=\{0,1,2,3,\ldots\}\) of natural numbers (see What is a natural number?). It is indeed quite simple to prove that the set \(\mathbb N\) is infinite, according to the given definition ! If such a demonstration exceeds the level of this article, one can however understand it intuitively: one sees hardly how one could establish a one-to-one correspondence of all the natural numbers with numbers \(1,\ldots,n\) by stopping at a certain \(n\): after having established this correspondence, one could always find a natural number greater than all those which one already counted…
In fact, the set \(\mathbb N\) is the prototype of infinite sets, in the sense that admitting its (theoretical) “existence” in set theory amounts to admitting the existence of infinite sets. Moreover, using rather simple methods as well, we can show that a set \(E\) is infinite if and only if it contains (a copy of) the set \(\mathbb N\) : this is our first characterisation of infinity. That a set \(E\) contains a “copy” of a set \(F\) simply means that there is a bijection between \(F\) and a subset of \(E\). Thus, with the elementary resources of naive set theory, we arrive at an already solid understanding of what mathematical infinity is: it “begins”, from the point of view of the “number of elements”, with the set \(\mathbb N\).
Thanks to this first characterisation, we can give many examples of infinite sets, because there are many natural bijections between the set \(\mathbb N\) and certain subsets of other natural sets. For example, the number sets \(\mathbb Z\) (integers), \(\mathbb Q\) (rational numbers), \(\mathbb R\) (real numbers) and \(\mathbb C\) (complex numbers) are all infinite because they “contain” the set \(\mathbb N\). Similarly a circle of non-zero radius is infinite, as is a non-empty open interval of the real line (e.g. a set of the form \(]a,b[=\{x\in \mathbb R : a<x<b\}\), for \(a<b\) real numbers). Another type of example concerns certain subsets of \(\mathbb N\) itself: thus, the set of even numbers is in bijection with \(\mathbb N\), as is the set of odd numbers, which gave rise to the illustration called “Hilbert’s hotel”, one version of which is the following. If a hotel with an infinite number of rooms numbered \(1,2,3,\ldots\) by the non-zero natural numbers is full, and a busload of tourists arrives with that many passengers, how is it possible to accommodate them all in the hotel? All you have to do is ask the occupant of the room numbered \(n\) to move into the room numbered \(2n\): this frees up all the odd-numbered rooms, and you can accommodate the new arrivals!
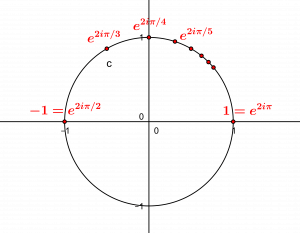
It can be shown that there is a bijection between the set \(\mathbb N\) and the set of points of the circle \(C\) noted as the complex numbers \(\{e^{2i\pi/(n+1)} : n\in\mathbb N\}\). Therefore, the circle is an infinite set
4.A secret of the mathematical universe: an intrinsic definition of infinity
But if we really want to penetrate the mystery of mathematical infinity, we must come up with an intrinsic characterisation, i.e. one that does not appeal to the finite or to an auxiliary set, even if it is \(\mathbb N\), “the first of the infinites”. This is what we are going to present here, and it does not require any more mathematical technology than the theory of bijections sketched above.
We have not rigorously defined what a subset of a set \(E\) is: if the elements of a set are the objects that “constitute” it, its subsets are its parts, that is, the sets \(S\) whose elements are all elements of \(E\). The key to the intrinsic characterisation of infinite sets lies in the extremely simple notion of proper subset: a subset \(S\) of a set \(E\) is said to be proper when it is not the whole set \(E\), i.e. when there is an element of \(E\) which is not an element of \(S\)…
From there, and using for example the first characterisation of infinite sets, we can prove the following theorem, which no longer makes any explicit reference to finite sets or natural numbers: a set \(E\) is infinite if and only if there exists a bijection between \(E\) and a proper subset of \(E\). In more intuitive terms, infinite sets are exactly those which “keep the same number of elements” when one removes one, or even a finite number, of elements. In fact, if we choose the elements well, we can even offload as many elements as there are in the set \(\mathbb N\) without reducing its size ! It is more or less obvious that a set which can be put in bijection with an infinite set is itself infinite; thus, any line of the Euclidean plane (see The Euclidean Plane: Ancient Geometry and the Analytical Approach), which can be put in bijection with the set \(\mathbb R\), is an infinite set.
Is this “intrinsic” characterisation a trick, since we propose to establish it from the first characterisation ? No: in mathematics one must always start from somewhere, and we started from the definition of the finite to define infinity; the second characterisation is therefore based on this definition. But like any characterisation, it can serve as an alternative definition: we could define an infinite set from this property – which mentions neither finite sets nor natural numbers – and define a finite set as being, this time, non-infinite. We would then have to show that a set is finite if and only if it can be counted… If this way of proceeding is very interesting in that it starts from a “pure” conceptualisation of mathematical infinity, it is however not very natural from the point of view of the initial intuition: in the order of knowledge, we start from the finite to go towards the infinite. But on the level of theory, it does not matter: it is possible to define infinity rigorously and simply, from the pure resources of naive set theory, and this is not the least achievement of mathematical science.
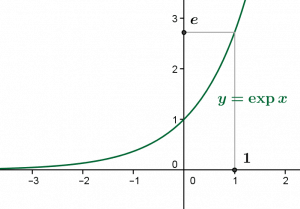
The exponential function, represented in part on this figure and whose base is the famous number \(e\), is a bijection between the set \(\mathbb R\) of real numbers and the proper subset \(\mathbb R_+^*\) of strictly positive real numbers. We thus see in another way that the set \(\mathbb R\) is infinite.
5.To infinity and beyond
Can the theory of mathematical infinity be so simple? Yes and no. What we have done here is to sketch out how one can define mathematical infinity, in the sense of what an infinite set is. But the theory has only just begun: just as not all finite sets have the same number of elements (there are in fact, as we have seen, an infinite number of different finite quantities), not all infinite sets have the same number of elements, in the sense of a “number of elements” which is itself derived from the notion of bijection, which can be applied indifferently to finite and infinite sets.
For example, it can be shown that the sets \(\mathbb N\), \(\mathbb Z\) and \(\mathbb Q\) have the “same number of elements”, whereas the sets \(\mathbb R\), \(\mathbb C\) and \(\mathbb H\) (the set of quaternions) for example, also have the same number of elements, but have more than the first three ! This requires a bit more resources, and that’s another story. Moreover, as in the case of finite quantities, there are an infinite number of different infinite quantities…
In “axiomatic set theory“, we learn to calculate with infinite quantities, ordinal or cardinal, which starts as a simple philosophical theory but has technical and complex developments. Closer to us, we can however quote to finish the following theorem (Cantor): if \(E\) is any set, finite or infinite, then the set \(P(E)\) of all subsets of \(E\) has strictly more elements than the set \(E\); in fact, if \(E\) is finite and has \(n\) elements, then \(P(E)\) has \(2^n\) elements.
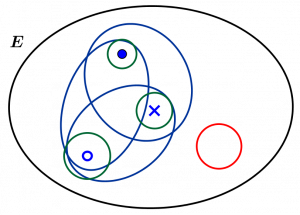
In the set \(E\), which has 3 elements, we have represented the different subsets: \(E\) itself, in purple the subsets with \(2\) elements, in green the one element subsets, and in red the empty set, the only subset with \(0\) element; in total, we have indeed \(1+3+3+1=8=2^3\) subsets. In an infinite set \(E\) of size \(k\), infinite cardinal, we can (at least under certain assumptions) make sense of the number \(2^k\) and show that the set \(P(E)\) of subsets of \(E\) has \(2^k\) elements.

0 Comments