by Jean Barbet | May 23, 2021 | Algebra, Geometry
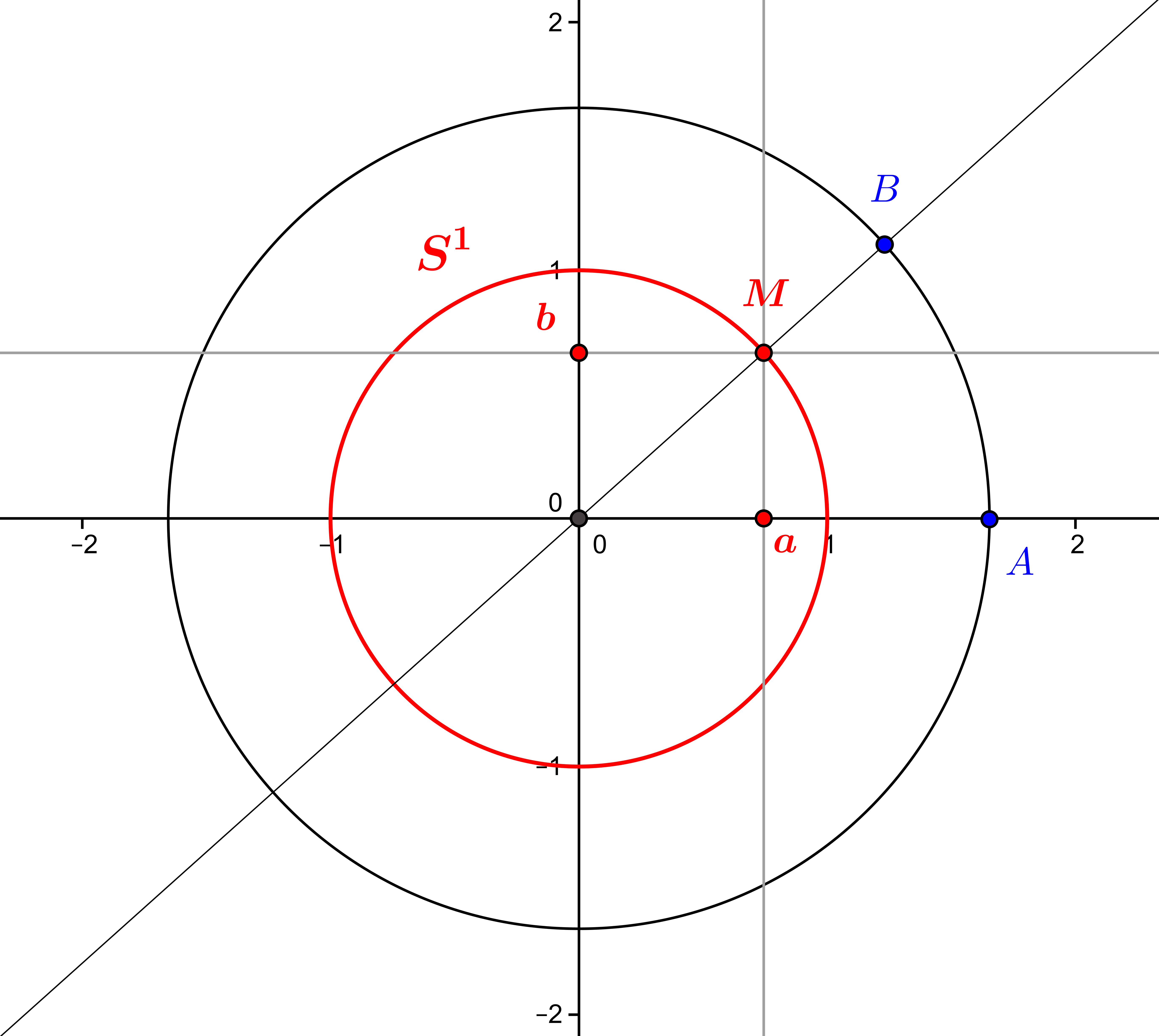
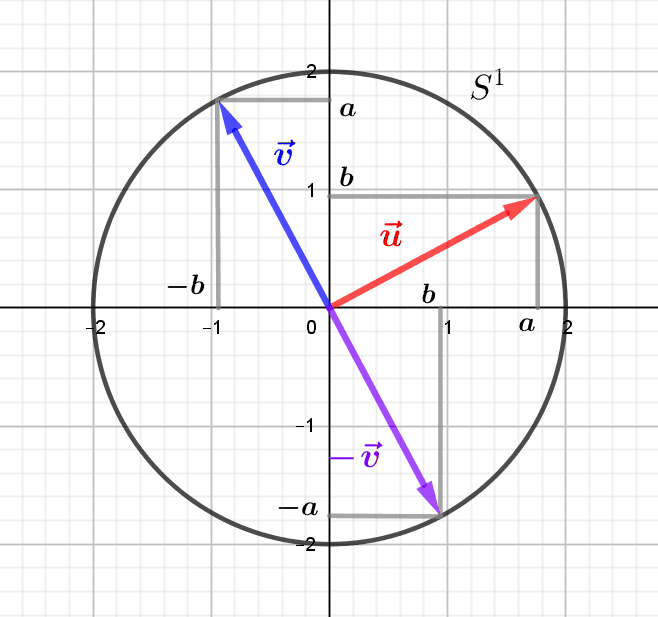
The linear transformations of the Euclidean plane are the invertible linear applications, i.e. of non-zero determinant. They allow us to move from one basis of the plane to another, and the orthogonal transformations, i.e. the vectorial isometries, exchange the...
by Jean Barbet | May 8, 2021 | Algebra, Geometry, Non classé
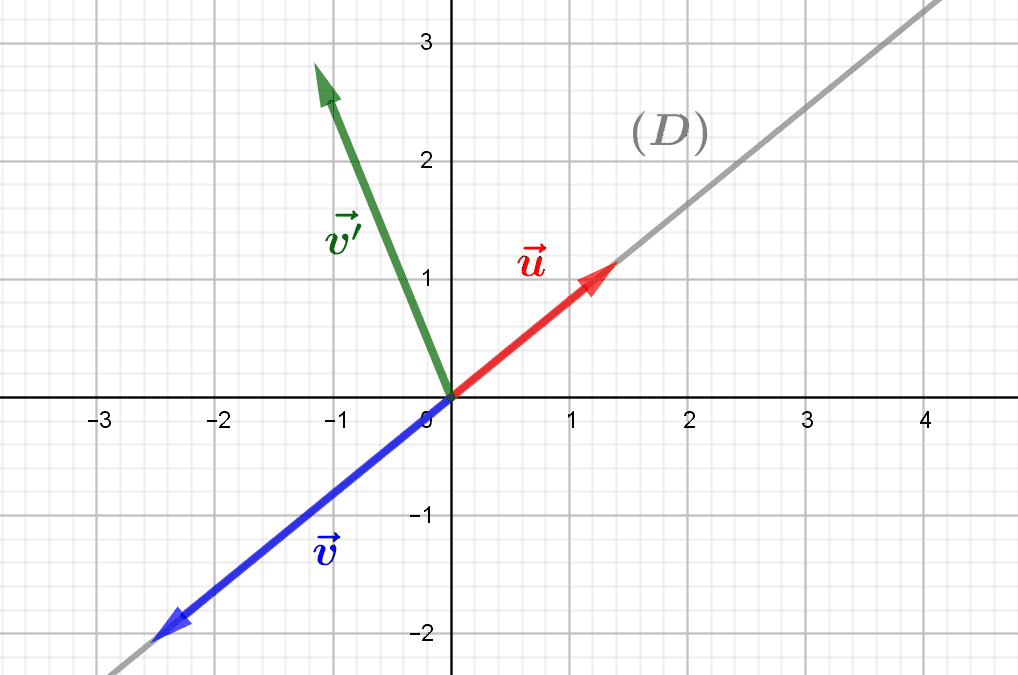
The representation of the Euclidean plane as the Cartesian product \(\mathbb R^2\) allows us to decompose any vector of the plane into two coordinates, its abscissa and its ordinate. This decomposition is linked to a particular and natural “representation...
by Jean Barbet | Feb 6, 2021 | Algebra, Geometry, Non classé
Vector angles are the usual oriented angles of Euclidean plane geometry. Thanks to the resources of naive set theory, they can be defined purely algebraically using an equivalence relation and the vectorial rotations of the plane. The operation of composing rotations...
by Jean Barbet | Oct 25, 2020 | Geometry, Non classé, Trigonometry
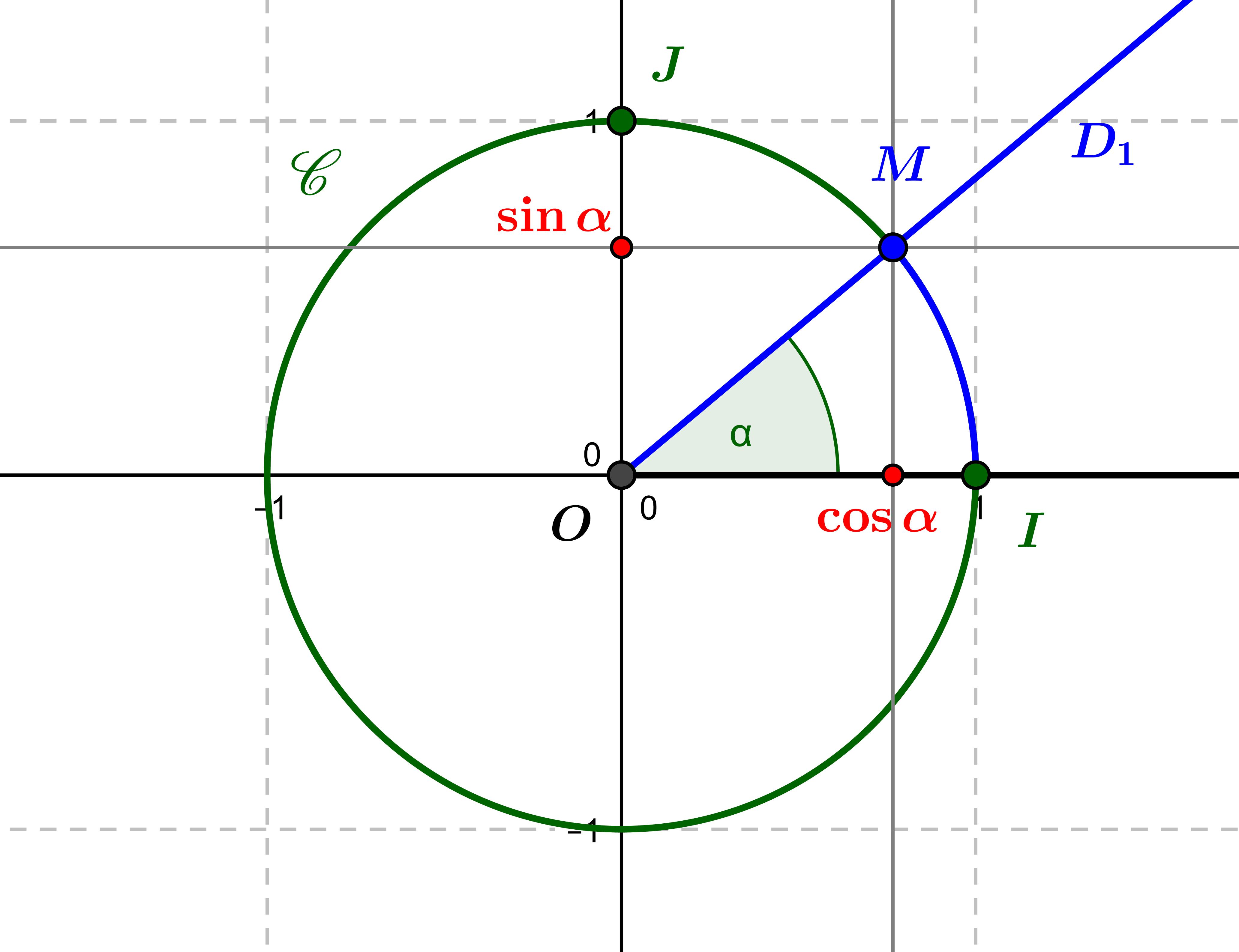
The trigonometric circle allows us to define the cosine, sine and tangent of an oriented angle, and to give an interpretation through Thales’ and Pythagoras’ theorems. Introduction: trigonometry and functions Trigonometry is the study of the relationships...
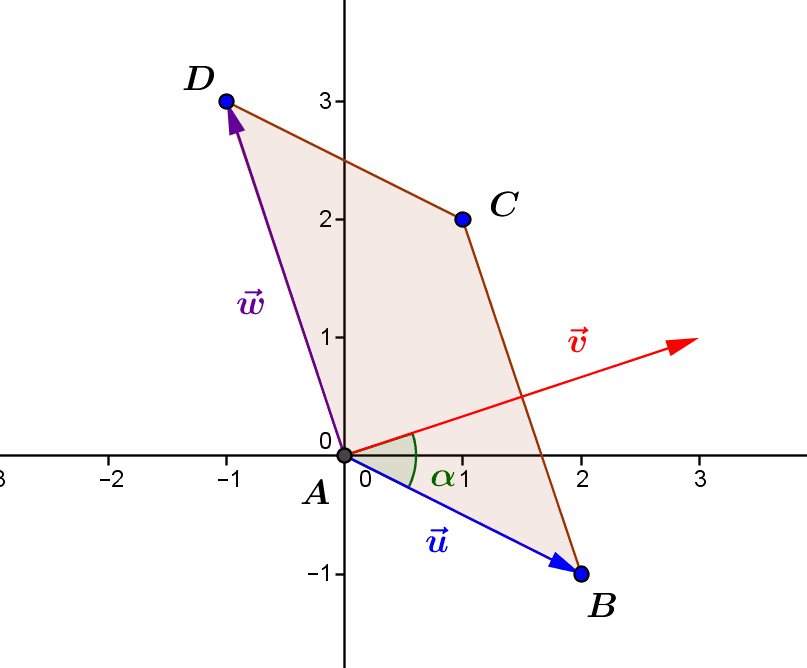
by Jean Barbet | Oct 4, 2020 | Algebra, Geometry
The scalar or dot product of two vectors in real space is a real number that takes into account the direction, sense and magnitude of both vectors. 1.The natural scalar product in the Euclidean plane 1.1.From the distance between two points to the scalar product In...
