Produits, relations, applications [C1.II.1]

1. Couples d’objets

Dans cette première section, nous voulons définir rigoureusement la notion de « couple d’objets », grâce aux ressources de la théorie naïve des ensembles, pour pouvoir définir la notion de « produit cartésien ». Nous donnerons une caractérisation de l’égalité de tels couples à partir de leurs éléments.

1.1. Définir les produits cartésiens

Nous allons introduire une nouvelle opération fondamentale sur les ensembles, d’une autre nature que l’intersection et l’union, celle de produit cartésien de deux ensembles, qui permettra d’aborder les notions de relation et de fonction (ou application).

L’adjectif « cartésien » vient du nom du mathématicien et philosophe français René Descartes, qui a introduit les (axes de) coordonnées dans sa description dite « analytique » de la géométrie plane, ce qui est l’archétype de cette construction.

Cette notion de produit cartésien sous-tend également la description ensembliste des relations, fonctions et opérations mathématiques telles que $$=,<,\leq,+,\times,\ln,\cos,\sin,\exp,\ldots.$$ Il est donc essentiel de l’assimiler proprement.

Par exemple, rappelons que pour deux entiers naturels $a,b$, on écrit $a\leq b$ quand $a$ est inférieur (ou égal) à $b$; il s’agit (pour l’instant) d’un concept intuitif, que nous représenterons, et ainsi conceptualiserons, comme un certain ensemble, en utilisant un produit cartésien.

L’idée, simple, est de considérer la relation $\leq$ à travers sa « table », c’est-à-dire l’ensemble $T$ de tous les « couples » $(a,b)$ d’entiers naturels $a,b$ tels que $a\leq b$.

La table de la relation $\leq$ entre entiers naturels est représentée sur la figure suivante.

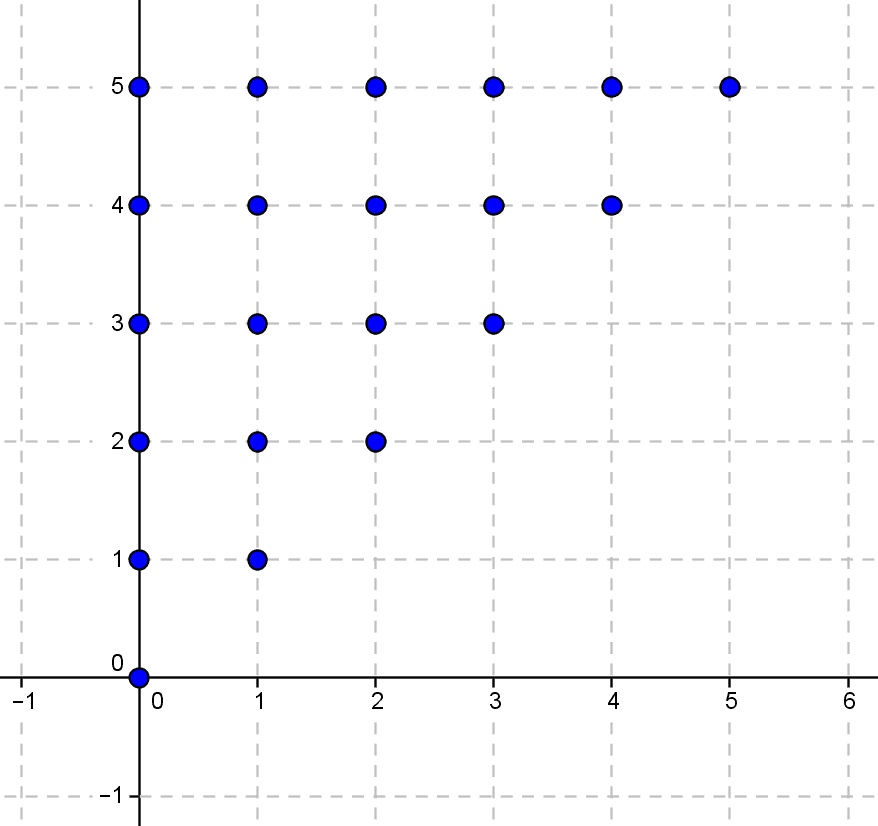
Nous pourrions introduire la notion de « couple » comme primitive : si $a,b$ sont deux objets, le « couple » $(a,b)$ est un objet « formé » des deux objets $a$ et $b$, dans cet ordre. Cependant, ceci serait redondant, puisque cette notion de couple peut être définie en utilisant la théorie des ensembles que nous connaissons déjà, comme nous allons le voir.

Notons d’abord que la notion intuitive de « couple » devrait respecter les contraintes suivantes :
i) Nous voulons distinguer le couple $(a,b)$ du couple $(b,a)$, autrement dit nous voulons conserver une trace de l’ordre (par exemple, on a $0\leq 1$, mais pas $1\leq 0$, donc $(0,1)$ est dans la table de $\leq$, tandis que $(1,0)$ n’y est pas)
ii) Si $(a,b)$ and $(a’,b’)$ sont deux couples d’objets tels que $(a,b)=(a’,b’)$, nous voulons que $a=a’$ et $b=b’$.

En fait, la condition (i) est une conséquence de la condition (ii), puisque si $a\neq b$ et (ii) est valide, alors $(a,b)\neq (b,a)$.

Une idée des plus naturelles serait de considérer l’ensemble $\{a,b\}$ comme le couple $(a,b)$. Cependant, les propriétés précédentes sont en défaut, puisqu’en général, on ne peut distinguer, dans les définitions par extension, les ensembles $\{a,b\}$ et $\{b,a\}$, qui sont toujours égaux par extensionnalité, puisqu’ils ont les mêmes éléments, $a$ et $b$, que $a=b$ ou non !

1.2. La notion ensembliste de couple d’objets

Heureusement, les ressources de la théorie des ensembles suffisent à conceptualiser rigoureusement cette notion, de la manière suivante.

Définition 1.1
Si $a$ et $b$ sont deux objets, le couple $(a,b)$ (ou la paire ordonnée $(a,b)$) est l’ensemble $\{\{a\},\{a,b\}\}$. L’objet $a$ est la première composante, l’objet $b$ est la seconde composante, du couple $(a,b)$.

Remarque 1.2
Notons qu’on fait ici un usage intuitif essentiel du concept d’objet, qu’on a considéré comme concept primitif dans le premier chapitre.

Cette définition peut sembler abstraite ou formelle au premier abord, mais elle permet de capturer ingénieusement et précisément le concept d’un couple d’objets, du moins tel qu’il a été esquissé et tel qu’on a besoin d’en faire usage en mathématique.

Par exemple, pour la première propriété, si $a\neq b$, alors le couple $(a,b)$ est différent du couple $(b,a)$ : en effet, on a $\{a\}\in (a,b)=\{\{a\},\{a,b\}\}$, tandis que $\{a\}\notin (b,a)=\{\{b\},\{a,b\}\}$ ! C’est bien sûr pour obtenir de telles propriétés qu’on définit ainsi le couple $(a,b)$.

Notons que si $a=b$, alors le couple $(a,a)$ est par définition l’ensemble $\{\{a\},\{a,a\}\}=\{\{a\},\{a\}\}$ (car $\{a,a\}=\{a\}$) $=\{\{a\}\}$. Cet ensemble ne contient qu’un élément, le singleton $\{a\}$.

En ce qui concerne la seconde propriété, nous l’énoncerons et la démontrerons ainsi :

Proposition 1.3
Si deux couples d’objets $(a,b)$ et $(a’,b’)$ sont égaux (comme ensembles), alors $a=a’$ et $b=b’$.

Démonstration
Nous distinguons deux cas : soit $a=b$, soit $a\neq b$. Si $a=b$, alors par définition et hypothèse, on a $\{\{a’\},\{a’,b’\}\}=(a’,b’)=(a,b)=\{\{a\},\{a,b\}\}=\{\{a\}\}$, et comme alors $\{a’,b’\}\in (a,b)$, on obtient $\{a\}=\{a’,b’\}$, car $\{a\}$ est le seul élément de $(a,b)$, et donc $a=a’=b’$ par extensionnalité (deux ensembles égaux ont par définition les mêmes éléments, voir le premier cours).
Si maintenant $a\neq b$, notons d’abord que le couple $(a,b)$ possède deux éléments distincts, $\{a\}$ et $\{a,b\}$. Comme $(a,b)=(a’,b’)$, on a $\{a’\}\in (a,b)$, et par ce qui précède soit $\{a’\}=\{a\}$, soit $\{a’\}=\{a,b\}$; comme $\{a,b\}$ a deux éléments par hypothèse (puisque $a\neq b$), la seconde possibilité est exclue, donc $\{a\}=\{a’\}$, et $a=a’$ par extensionnalité. Nous avons aussi $\{a’,b’\}\in (a’,b’)=(a,b)$, donc soit $\{a’,b’\}=\{a\}$, soit $\{a’,b’\}=\{a,b\}$; si $\{a’,b’\}=\{a\}$, alors $a=a’=b’$ et $(a,b)=(a’,b’)=(a’,a’)$ a un élément, $\{a’\}$, ce qui est exclu à nouveau; on obtient donc $\{a’,b’\}=\{a,b\}$. Comme maintenant $b’\in \{a,b\}$, soit $b’=a$, soit $b’=b$; si $b’=a$, alors $a=a’=b’$ et à nouveau $(a,b)=(a’,b’)$ possède un seul élément, ce qui est impossible. Par conséquent, on a $b=b’$ et la démonstration est terminée. $\square$

Remarque 1.4
i) Cette preuve est très détaillée, et nous supprimerons progressivement certains éléments évidents des arguments, pour ne pas surcharger le texte. L’étudiant(e) doit apprendre à interpréter les démonstrations en suppléant aux non-dits évidents.
ii) La démonstration utilise plusieurs raisonnements par cas et plusieurs raisonnements par l’absurde imbriqués. Il est normal d’éprouver de la difficulté à le suivre en entier la première fois. On apprend en faisant, et l’étude détaillée et la reproduction des preuves sont des étapes essentielles.
iii) Nous avons utilisé la signification intuitive des entiers naturels $1$ et $2$ dans le comptage des éléments de certains ensembles, ce qu’il n’est pas possible d’éviter, et illustre ce que nous voulions dire dans le premier cours lorsque nous affirmions que les entiers naturels sont des concepts primitifs en mathématique.

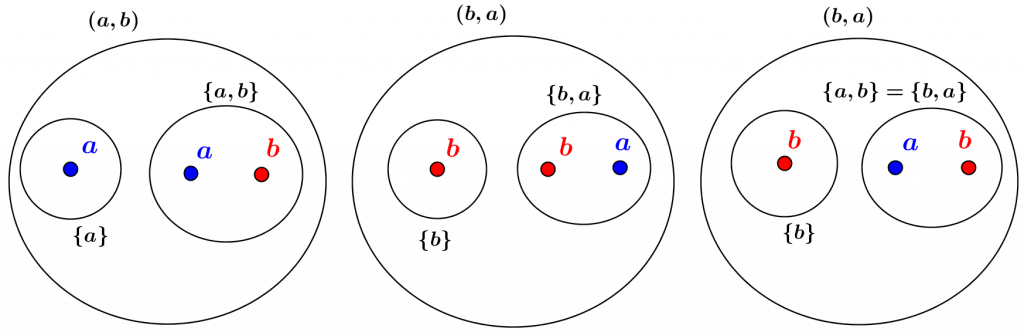
La figure suivante propose une représentation des couples et des singletons qu’on peut former avec deux éléments.

1.3. Exercices

Exercice 1.5
i) Soient $E=\{1,3,5,7\}$ et $F=\{2,4,6,8\}$. Ecrire tous les couples d’objets $(a,b)$ qu’on peut former avec $a\in E$ et $b\in F$. Faire la même chose avec $a\in F$ et $b\in E$.
ii) Ecrire une preuve détaillée de la première propriété des couples d’objets (c’est-à-dire que si $a\neq b$, alors $(a,b)\neq (b,a)$), comme corollaire de la proposition.
iii) Si $a,b,c$ sont trois objets, le triplet $(a,b,c)$ est par définition le couple $((a,b),c)$. Lister tous les éléments de $(a,b,c)$, qui sont des ensembles, puis les éléments de ses éléments.

2. Produits et relations

2.1. Produits cartésiens

4. Opérations élémentaires sur les relations et applications

4.1. Restriction et co-restriction

Si $E$ et $F$ sont deux ensembles et $R$ est une relation entre $E$ et $F$, nous avons insisté sur le fait que stricto sensu la relation $R$ est la donnée des trois ensembles $E$, $F$ et $R$, soit du triplet $(E,F,R)$, et nous avons donné des exemples où la « même » description d’une relation par son graphe donnait lieu à des relations différentes, lorsque le domaine ou le co-domaine étaient différents.

Il est important de bien comprendre ceci et de ne pas le considérer comme un formalisme stérile, ou comme du pédantisme. Il est en effet souvent nécessaire de définir de nouvelles relations ou de nouvelles applications en modifiant seulement le domaine ou le co-domaine, ce qu’on appelle restriction ou co-restriction d’une relation ou d’une application.

Nous l’avons déjà pratiqué sans le dire en définissant la « restriction » d’une relation (exercice 2.9(viii)), la « co-restriction » d’une application (exemple 3.5(ii)) et une application à partir d’une relation fonctionnelle (exercice 3.7(i)).

Ici, nous donnons des définitions rigoureuses qui ne devraient poser aucun problème à l’étudiant(e) qui a suivi attentivement le cours jusqu’ici.

4.2. Restriction d’une relation ou d’une application

Définition 4.1
Soit $(E,F,R)$ une relation. Si $S\subseteq E$ est une partie de $E$, la restriction de $R$ à $S$ est la relation de $S$ dans $F$ décrite par le triplet $(S,F,R_{|_S})$, autrement dit dont le graphe est le sous-ensemble $R_{|S}=\{(x,y)\in R : x\in S\}$ de $S\times F$.

Autrement dit, pour une relation $R$ entre un ensemble $E$ et un ensemble $F$, la restriction de $R$ à un sous-ensemble $S$ de $E$ consiste précisément à « restreindre » la relation $R$ aux seuls couples $(x,y)$ pour lesquels $x$ est un élément de $S$.

La restriction d’une relation a donc trait au domaine de cette relation.

Etant donné qu’une application est un cas particulier de relation, nous pouvons ici appliquer directement la notion de restriction à une application. Si $f:E\to F$ est une application, la restriction de $f$ à un sous-ensemble $S$ de $E$ est tout simplement l’application notée $f_{|S}:S\to F$, et dont la description est $(S,F,R_{|S})$, si la description de $f$ est $(E,F,R)$.

La restriction d’une application est donc sa restriction comme relation.

Exemple 4.2
i) Si $|$ est la relation de divisibilité sur l’ensemble $\mathbb Z\times\mathbb N$, c’est-à-dire le triplet $(\mathbb Z,\mathbb N,R)$, où $R=\{(n,m)\in \mathbb Z\times\mathbb N : n|m\}$, alors la restriction de $|$ à $\mathbb N\subseteq\mathbb Z$ est la relation de divisibilité sur $\mathbb N\times\mathbb N$.
ii) Si $+:\mathbb R\times\mathbb R\to \mathbb R$ est l’addition des nombres réels, alors comme le produit $\mathbb N\times\mathbb N$ est un sous-ensemble de $\mathbb R\times\mathbb R$, on peut définir la restriction de $+$ à $\mathbb N\times\mathbb N$, comme l’application $+_{\mathbb N\times\mathbb N}:\mathbb N\times\mathbb N\to \mathbb R$, $(m,n)\mapsto m+n$. Comme opération, il s’agit bien de l’addition des entiers naturels mais attention : c’est une application différente de l’addition $+:\mathbb N\times\mathbb N\to \mathbb N$ (on utilise la même notation par abus), car les co-domaines sont différents ! On peut bien sûr, dans cet exemple, remplacer $\mathbb N$ par $\mathbb Z$ ou $\mathbb Q$ par exemple.

Remarque 4.3
Nous avons parlé de relations binaires sur un ensemble $E$, comme relations de $E$ dans $E$ et en toute rigueur on devrait définir la restriction à $S$ d’une telle relation comme la relation de graphe $\{(x,y)\in S\times E : (x,y)\in R\}$. Cependant, il arrive qu’on entende par « restriction » de $R$ à $S$ la relation binaire $(S,S,R’)$ sur $S$ telle que $R’=\{(x,y)\in S\times S : (x,y)\in R\}$ ! Autrement dit, on fait aussi une restriction sur le co-domaine, qui est $E$ lui-même. C’est dans ce sens où nous l’avons pris dans la section sur les relations.

Cette confusion terminologique, regrettable, est en général levée par le contexte. Lorsqu’on considère des relations binaires sur des ensembles (et donc où le domaine et le co-domaine sont identiques), il est naturel d’appliquer la restriction aux deux.

Exemple 4.4
Si $\leq$ est la relation binaire d’ordre large sur $\mathbb R^2$, et si $E$ est l’un des ensembles $\mathbb N,\mathbb Z$ ou $\mathbb Q$, alors on obtient par « restriction » de $\leq$ à $E$ la relation binaire d’ordre large usuelle sur $E$.

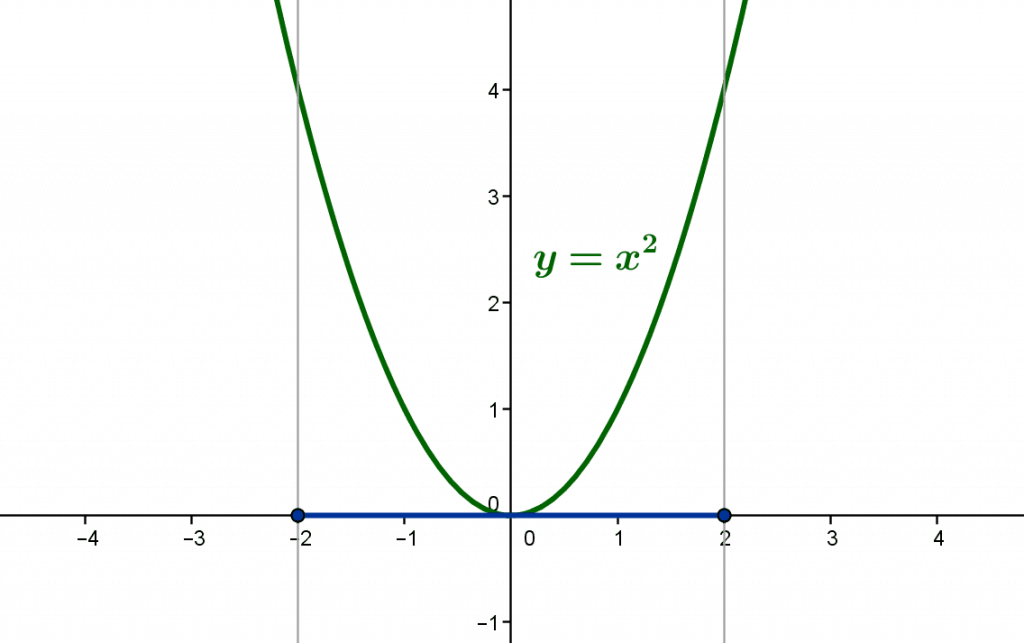
Sur la figure suivante est représentée la restriction de la fonction $x\mapsto x^2$ au réel segment $[-2,2]$.

4.3. Co-restriction d’une relation ou d’une application

Si la restriction consiste à rapporter une relation à un sous-ensemble de son domaine, la co-restriction consiste naturellement à rapporter une relation à un sous-ensemble de son co-domaine.

Définition 4.5
Soit $(E,F,R)$ une relation. Si $T\subseteq F$ est une partie de $F$, la co-restriction de $R$ à $T$ est la relation $(E,T,R^{|T})$ entre $E$ et $T$, dont le graphe est $R^{|T}=\{(x,y)\in R : y\in T\}$.

Autrement dit, pour une relation $R$ entre deux ensembles $E$ et $F$, la co-restriction de $R$ à un sous-ensemble $T$ de $F$ consiste précisément à « restreindre » la relation $R$ aux seuls couples $(x,y)$ pour lesquels $y$ est un élément de $T$.

La co-restriction d’une relation a donc trait au co-domaine de cette relation.

Une application étant un cas particulier de relation, nous pouvons appliquer la définition de co-restriction à une application $f:E\to F$. Mais attention : si la co-restriction de $f$ à un sous-ensemble $T$ de $F$ est bien définie comme relation, ce n’est pas toujours une application, car un élément de $E$ n’a pas toujours un correspondant par $f$ dans $T$ !

Exemple 4.6
i) Si $|$ est la relation de divisibilité sur l’ensemble $\mathbb N\times\mathbb Z$, c’est-à-dire le triplet $(\mathbb N,\mathbb Z,R)$ où $R=\{(n,m)\in\mathbb N\times \mathbb Z : n|m\}$, alors la co-restriction de $|$ à $\mathbb N\subseteq \mathbb Z$ est la relation de divisibilité sur $\mathbb N\times\mathbb N$.
ii) Si $+_{|\mathbb N}:\mathbb N\times\mathbb N\to \mathbb R$ est l’addition des entiers naturels, considérée comme restriction de l’addition $+:\mathbb R\times\mathbb R\to\mathbb R$ des nombres réels (voir l’exemple du paragraphe précédent), alors la co-restriction de $+_{|\mathbb N}$ à $\mathbb N\subseteq\mathbb R$ est l’addition usuelle $+_\mathbb N:\mathbb N\times\mathbb N\to\mathbb N$ des entiers naturels. Dans ce cas, il s’agit bien d’une application.
iii) Si $s:\mathbb N\to\mathbb N, n\mapsto n+1$ est l’application « successeur », que nous avons déjà rencontrée, le graphe $R$ de la co-restriction $s^{|P}$ de $s$ au sous-ensemble $P$ de $\mathbb N$ des entiers naturels pairs est l’ensemble des couples $(m,n)$ d’entiers naturels tels que $n=m+1$ et $n$ est pair. Cette co-restriction n’est donc pas une application, puisque pour aucun entier naturel $m$ pair il n’existe d’entier naturel $n$ tel que $(m,n)\in R$ : en effet, si $m$ est pair, $m+1$ est toujours impair !

Nous verrons dans la suite du cours comment il est possible de s’assurer que la co-restriction d’une application $f:E\to F$ est une application. Comme l’étudiant(e) l’aura peut-être deviné, cela revient à ce que le sous-ensemble $T$ auquel on veut appliquer la co-restriction contienne tous les éléments de $F$ de la forme $f(x)$, pour $x\in E$. Nous introduirons des définitions spécifiques pour préciser cette idée.

4.4. Exercices

Exercice 4.7
i) On considère l’application $f:\mathbb Z\times\mathbb N^*\to \mathbb Z\times \mathbb N$ qui associe à un couple $(n,m)\in\mathbb Z\times\mathbb N^*$ le couple $(q,r)\in \mathbb Z\times\mathbb N$ où $q$ est le quotient et $r$ le reste de la division euclidienne de $n$ par $m$ (voir l’exercice 3.7(iii)). Décrire un sous-ensemble $S$ de $\mathbb N$, le plus petit possible, tel que la co-restriction de $f$ à $\mathbb Z\times S$ est encore une application.
ii) On note $g:\mathbb N\times\mathbb N^*\to \mathbb N\times\mathbb N$ l’application définie comme l’application $f$ au (i). Comment obtenir $g$ à partir de $f$ par une ou des opérations sur $f$ ? Si on pose la même question pour $g$ que pour $f$, le sous-ensemble $S$ de $\mathbb N$ trouvé au (i) convient-il ici ?
iii) Soit $f:\mathbb R\to\mathbb R$ la valeur absolue (voir le premier chapitre), c’est-à-dire $f(x)=|x|$ pour tout $x\in \mathbb R$, avec $|x|=x$ si $x\geq 0$, $|x|=-x$ si $x\leq 0$. On considère la restriction $g=f|_{\mathbb Q}$ de $f$ à $\mathbb Q\subseteq \mathbb R$. Trouver un sous-ensemble $S$ de $\mathbb R$, différent de $\mathbb R$ et ne contenant pas $\pi$, tel que la co-restriction de $g$ à $S$ est une application.
iv) Soit $f:E\to F$ une application. Montrer que pour tout sous-ensemble $T$ de $F$, la co-restriction de $f$ à $T$ est une relation fonctionnelle.

5. Composition des applications