[Archive] Arithmétique naturelle [Ancien C1.III.2]

1. Division euclidienne dans l’ensemble $\mathbb N$

A l’école primaire, nous apprenons à diviser un entier naturel $a$ par un autre entier naturel $b$ non nul : le résultat est donné en général sous la forme d’un quotient $q$ et d’un reste $r$ sous la forme $a=b\times q+r$ avec $r<b$, et $r$ est nul exactement lorsque $a$ est divisible par $b$. En revanche, lorsque $r\neq 0$ la division euclidienne ne donne qu’une approximation de la division de $a$ par $b$.

L’interprétation intuitive de la division euclidienne, sur le plan des quantités, est la suivante : combien de fois $b$ est-il « contenu » dans $a$ ? Ou encore : étant donnée une collection de $a$ objets, quel est le nombre maximal $q$ de « paquets » de $b$ objets qu’on peut faire avec ceux-ci ? Ce nombre est maximal exactement lorsque, une fois les « paquets » rassemblés, les objets restant éventuellement ne permettent pas de former un nouveau paquet, leur nombre $r$ étant donc strictement inférieur à $b$.

Nous reconstruisons ici la théorie de la division euclidienne en utilisant nos nouveaux concepts mathématiques et les axiomes du successeur dans $\mathbb N$, et nous lui donnons ainsi un fondement numérique solide qui ne dépend plus de l’intuition des ensembles $\mathbb Z,\mathbb Q$ et $\mathbb R$ comme dans le Chapitre 1 (Entrer dans l’univers mathématique).

Nous pouvons traduire l’interprétation précédente sur le plan de la théorie des ensembles finis comme suit : combien d’ensembles deux-à-deux disjoints de $b$ éléments pouvons-nous former avec un ensemble de $a$ éléments ? Si $a$ est un multiple de $b$, disons $a=b.d$, alors la réponse est $d$, bien sûr, mais en général $a$ n’est pas divisible par $b$, donc il nous faut obtenir la « meilleure approximation ».

Nous aurons pour ceci besoin de résultats auxiliaires sur le « plus grand élément » et le « plus petit élément » de certains sous-ensembles de $\mathbb N$ (on pourra se reporter au cours \no 2 pour la théorie des ensembles finis et de leur cardinal).

Lemme 1
Tout sous-ensemble fini $S$ non vide de $\mathbb N$ possède un plus grand élément, autrement dit il existe $n\in S$ tel que pour tout $m\in S$, on ait $m\leq n$.

Démonstration
On procède par récurrence sur le cardinal $k$ de $S$. Si $k=1$, alors $S$ ne possède qu’un élément $n$, qui est nécessairement le plus grand élément de $S$. Supposons que la propriété est vérifiée pour les sous-ensembles finis de cardinal $k>1$, et que $|S|=k+1$. Soit $i\in S$ un élément quelconque : l’ensemble $S-\{i\}$ est fini et possède $k$ éléments (Cours \no 3, chapitre 2), donc par hypothèse de récurrence il possède un plus grand élément, appelons-le $m$. Soit alors $n$ le plus grand des deux nombres $i$ et $m$, par [Axiomes et structure de l’ensemble $\mathbb N$, proposition 8], et soit $j\in S$ : si $j=i$, alors on a $j\leq n$, tandis que si $j\neq i$, par définition de $m$ on a $j\leq m\leq n$. Il s’ensuit que $n$ est le plus grand élément de $S$, et le lemme est démontré par récurrence.$\square$

Exemple 1
L’ensemble $2\mathbb N$ des entiers naturels pairs (c’est-à-dire multiples de $2$) est infini, donc il ne possède pas de plus grand élément (par contraposée du lemme 1). En effet, si $n\in 2\mathbb N$, $n$ est de la forme $2.m$ pour $m\in\mathbb N$, et on a $n=2.m.<2.(m+1)\in 2\mathbb N$.

Proposition 1
Tout sous-ensemble non vide $S$ de $\mathbb N$ possède un plus petit élément, autrement dit il existe $n\in S$ tel que pour tout $m\in S$, on a $n\leq m$.

Démonstration
Distinguons deux cas. Dans le premier, si $0\in S$ alors $0$ est évidemment le plus petit élément de $S$. Dans le second, on suppose que $0\notin S$, et on considère alors l’ensemble $X$ de tous les entiers naturels qui sont strictement plus petits que tous les éléments de $S$, c’est-à-dire $X=\{i\in \mathbb N : \forall m\in S,\ i< m\}$. Par hypothèse, $X$ n’est pas vide, puisque $0\in X$. Comme $S$ n’est pas vide non plus, il existe $a\in S$, si bien que $X\subseteq [[0,a]]=\{n\in\mathbb N : n\leq a\}$, donc $X$ est fini comme sous-ensemble d’un ensemble fini (section [Sous-ensembles d’un ensemble fini], Corollaire 2). Par le lemme 1, $X$ possède un plus grand élément, notons-le $k$. Par définition de $X$ et de $k$, pour tout $m\in S$ on a donc $k<m$, soit, par [Axiomes et structure de l’ensemble $\mathbb N$, exercice 4(i)], $k+1\leq m$. Comme $k+1\in S$, il s’ensuit que $k+1$ est le plus petit élément de $S$. $\square$

Remarque 1
Cette propriété de l’ordre naturel sur $\mathbb N$ concerne tous les sous-ensembles de $\mathbb N$, et est à la base de la représentation de $\mathbb N$, avec la relation $<$, comme un ordinal, c’est-à-dire la version formelle d’un nombre infini conçu comme un « type d’ordre ». La proposition 1 est en fait équivalente au principe de récurrence (voir les exercices).

Théorème 1 [Division euclidienne]
Si $a$ et $b$ sont deux entiers naturels tels que $b\neq 0$, alors il existe deux entiers naturels $q$ et $r$ uniques, tels que $a=b.q+r$ et $r<b$. Les nombres $q$ et $r$ sont appelés respectivement le quotient et le reste de la division euclidienne de $a$ par $b$.

Démonstration
Nous démontrons d’abord l’existence de $q$ et de $r$. Soit $b\mathbb N$ l’ensemble des multiples de $b$, explicitement $b\mathbb N=\{b.d : d\in\mathbb N\}$, image de l’application $M_b:\mathbb N\to \mathbb N$, $d\mapsto b.d$ de « multiplication par $b$ ». L’ensemble $[[0,a]]=\{n\in\mathbb N : n\leq a\}$ est fini (voir le cours \no 3, chapitre 2), donc le sous-ensemble $b\mathbb N\cap [[0,a]]$ est fini également (idem); n’étant pas vide puisqu’il contient $0=b.0$, il possède alors un plus grand élément $k$ par le lemme 1, qui est de la forme $b.q$.
Par définition de $k$, on a $b.q\leq a$, donc par définition de $\leq$ il existe un entier naturel $r$ tel que $a=b.q+r$. Supposons par l’absurde que l’on a $r\geq b$ : par les propriétés de $\leq$ (voir [Axiomes et structure de l’ensemble $\mathbb N$, proposition 6(iv)]), on obtient $a=b.q+r\geq b.q+b=b.(q+1)$, ce qui entraîne que $b.(q+1)\in b\mathbb N\cap [[0,a]]$; comme $k=bq<b(q+1)=bq+b$, ceci contredit la définition de $k$, donc par reductio ad absurdum, on a $r<b$ et l’existence de $q$ et de $r$ est démontrée.
En ce qui concerne leur unicité, supposons que $q’,r’\in\mathbb N$ sont tels que $a=b.q’+r’$ avec $r'<b$; on obtient $b.q’\leq a <b.q’+b=b.(q’+1)$, donc $q’$ est le plus grand élément de $b\mathbb N\cap [[0,a]]$, soit $q=q’$, et $b.q+r=b.q+r’$; par [Axiomes et structure de l’ensemble $\mathbb N$, lemme 1(i)], on obtient $r=r’$, et le théorème est démontré. $\square$

Remarque 2
Dans la démonstration de cet énoncé dans le cours \no 1, nous avons utilisé les propriétés intuitives de la soustraction dans l’ensemble $\mathbb Z$ et de la valeur absolue dans l’ensemble $\mathbb R$. Ici la propriété de simplifiabilité de l’addition dans $\mathbb N$ permet de se passer de la soustraction, tandis que l’usage du plus grand élément d’un ensemble fini permet de se passer de la valeur absolue.

La figure suivante représente représente une division euclidienne par « paquets ».

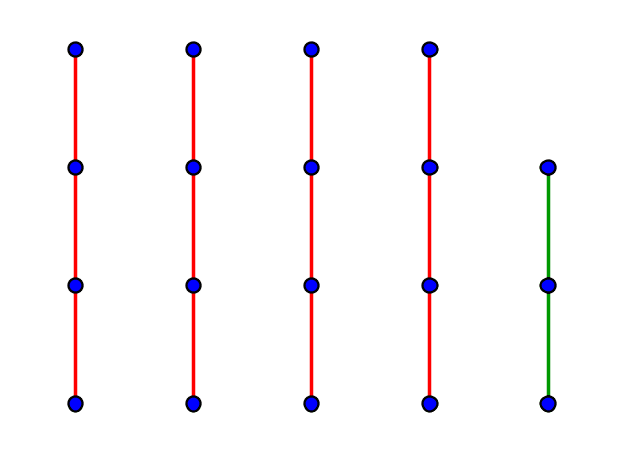
Définition 1
Si $a$ et $b$ sont deux entiers naturels avec $b>0$, on dit que $a$ est le dividende et $b$ le diviseur de la division euclidienne $a=b.q+r$.

Exemple 2
On a $527=48\times 10+47$; comme $47<48$, $10$ est le quotient et $47$ est le reste, de la division euclidienne de $527$ (dividende) par $48$ (diviseur).

Corollaire 1
Si $a$ et $b$ sont deux entiers naturels, avec $b\neq 0$, alors $b$ divise $a$ si et seulement si le reste de la division euclidienne de $a$ par $b$ est $0$.

Démonstration
Si $b|a$, alors il existe par définition $d\in\mathbb N$ tel que $a=b.d=b.d+0$, donc par unicité du quotient et du reste dans la division euclidienne de $a$ par $b$, $d$ est le quotient, et $0$ est le reste, de cette division. Inversement, écrivons la division euclidienne de $a$ par $b$ sous la forme $a=b.q+r$, avec $r<b$ : si $r=0$, on a $a=b.q$, donc $b|a$. $\square$

Remarque 3
Ce corollaire peut paraître évident, à cause de l’intuition de ce que signifie la division euclidienne, mais il est nécessaire de le démontrer.

Un entier naturel $d$ tel que $d$ divise $n$ est appelé un diviseur de $n$, et $n$ est alors appelé un multiple de $d$.

1.1 Exercices

Exercice 1
i) Démontrer par l’absurde le principe de récurrence à partir des deux premiers axiomes de Peano et de la proposition 1. Indication : si $S\subseteq \mathbb N$ est un sous-ensemble tel que $0\in S$ et $s(n)\in S$ dès que $n\in S$, supposer que $S\neq \mathbb N$, et considérer le plus petit élément du sous-ensemble non vide $\mathbb N-S$ de $\mathbb N$.
ii) Effectuer la division euclidienne de $247$ par $53$.
iii) Quel est le reste dans la division euclidienne de $114$ par $3$ ?
iv) Soient $a,b\in\mathbb N$, avec $b>0$. Supposons que $a<b$; quels sont le quotient et le reste de la division euclidienne de $a$ par $b$ ?
v) Soient $a,b\in\mathbb N$, avec $a>0$ et $b>1$. Montrer qu’il existe un unique entier naturel $n$ tel que $b^n\leq a<b^{n+1}$.

2. Les nombres premiers