Le nombre d’éléments [C1.II.2]

Rappelons que si $R$ est une relation entre deux ensembles $E$ et $F$, la relation inverse ou opposée de $R$ est la relation de $F$ dans $E$, notée $R^o$, et dont le graphe est $\{(y,x)\in F\times E : (x,y)\in R\}$.

Dans la première section, nous avons traité des relations fonctionnelles et des applications, et nous avons évoqué le caractère « orienté » d’une application : pour une application $f:E\to F$ de graphe $R$, on peut identifier, par définition, pour chaque $x$ de $E$, un unique $y\in F$ tel que $(x,y)$ est dans $R$.

Cette propriété n’est pas toujours préservée par la relation opposée. Par exemple, la fonction successeur $s:\mathbb N\to\mathbb N$ est une application, et si $R=\{(m,n)\in\mathbb N^2 : n=m+1\}$ désigne son graphe, alors il n’existe pas d’entier naturel $n$ tel que $(0,n)\in R^o$, autrement dit tel que $(n,0)\in R$ : $R^o$ ne définit donc pas une application. On a mis en défaut {l’existence} systématique d’un correspondant pour $R^o$.

Pour un contre-exemple ayant trait à la fonctionnalité, considérons l’addition $+:\mathbb R^2\to \mathbb R$ décrite comme application, de graphe $A=\{((m,n),p)\in (\mathbb N^2\times \mathbb N) : m+n=p\}$. On a $0+3=3=1+2$, donc les deux triplets $((0,3),3)$ et $((1,2),3)$ sont éléments de $A$ : comme nous l’avons déjà évoqué, un entier naturel donné peur avoir {plus d’un antécédent} pour l’addition, si bien que la relation opposée $A^o$ sur $\mathbb R\times\mathbb R^2$ ne définit pas une application, puisqu’un élément donné de $\mathbb R$ peut avoir plusieurs correspondants par $A^o$. On a mis en défaut l‘unicité systématique d’un correspondant par $A^o$.

Dans cette section nous construisons progressivement la notion de bijection entre deux ensembles, qui permet de formaliser l’idée que deux ensembles puissent avoir le même nombre d’éléments, que ces ensembles soient finis ou non.

Cette notion correspond précisément à l’idée d’une application dont la relation opposée est elle-même une application : on peut intuitivement mettre en correspondance « un-à-un » les éléments d’un ensemble et d’un autre.

De même qu’il existe deux composantes dans l’idée d’application, celle de relation fonctionnelle (unicité d’un correspondant) et celle d’existence d’un correspondant, nous pouvons décomposer la notion de bijection en deux notions essentielles, celles d’injection ou application injective, et celle de surjection ou application surjective, qui s’interprètent également en termes de « nombre d’éléments ».

1. Applications injectives et surjectives

Nous considérons à nouveau l’application successeur $s:\mathbb N\to\mathbb N$, $n\mapsto n+1$. Supposons que $m,n$ sont deux entiers naturels tels que $s(m)=s(n)$ : autrement dit, on a $m+1=n+1$ et intuitivement, $m$ est le plus grand entier naturel strictement inférieur à $s(m)$, et $n$ le plus grand entier naturel strictement inférieur à $s(n)$, et comme ces derniers sont égaux, on a $m=n$.

Une autre façon de le voir est d’utiliser la propriété dite de simplifiabilité de l’addition des entiers naturels : si $m,n,p$ sont trois entiers naturels tels que $m+p=n+p$, alors $m=n$. Alors, si $s(m)=s(n)$, c’est que $m+1=n+1$, donc $m=n$ ! Toutefois, nous ne définirons qu’ultérieurement l’addition à partir des propriétés de la fonction successeur, dans le cours sur l’ensemble $\mathbb N$ des entiers naturels. A moins donc d’admettre la simplifiabilité de $+$ comme un postulat, nous nous appuyons sur l’intuition de la fonction successeur.

Ceci montre qu’un entier naturel $n$ a toujours au plus un antécédent par la fonction $s$, même si par définition, $0$ n’a pas d’antécédent. Cette propriété, qui est en quelque sorte la propriété « duale » de la fonctionnalité du graphe d’une application, nous mène à la définition suivante, qui formalise l’idée de l’unicité systématique d’un antécédent par une application.

Définition 1.1
Si $E$ et $F$ sont deux ensembles, une application $f:E\to F$ est dite injective, ou est appelée une injection, si pour tous $x,x’\in E$ tels que $f(x)=f(x’)$, on a $x=x’$ (autrement dit, si deux éléments du domaine de $f$ qui ont la même image sont égaux).

Cette définition est une reformulation rigoureuse de la propriété : « tout élément du co-domaine de $f$ a au plus un antécédent par $f$ », en disant que « si deux éléments du domaine de $f$ ont la même image par $f$, alors ils sont égaux ».

Il est habituel en mathématique d’avoir à reformuler des notions ou des propriétés intuitives sous une forme moins intuitive ou moins directe, pour obtenir une expression rigoureuse, dépourvue d’ambiguïté, qui est susceptible d’une utilisation plus claire dans les descriptions et démonstrations mathématiques.

Le successeur est notre exemple fondamental d’application (ou fonction) injective, et nous en verrons de nombreux autres. Nous avons mentionné précédemment que les opérations $+$ et $\times$, sur $\mathbb R$ ou l’un quelconque des sous-ensembles $\mathbb N$, $\mathbb Z$ ou $\mathbb Q$, ne sont pas injectives, puisque certains éléments du co-domaine possède plusieurs antécédents.

Donnons un exemple non-mathématique instructif.

Exemple 1.2
Soient $F$ l’ensemble des adultes français et $S:F\to \mathbb N$ l’application qui associe à un adulte $a\in S$ son numéro de sécurité sociale (autrement dit, le graphe de $S$ est l’ensemble des couples $(a,n)$, où $n$ est le numéro de sécurité sociale de $a$). Toute personne possède un unique tel numéro, donc $S$ est bien une application, et deux adultes différents ont des numéros de sécurité sociale différents, sinon ces numéros n’ont aucune utilité. Par contraposée, si deux personnes ont le même numéro de sécurité sociale, « ils sont la même personne ». Autrement dit, l’application $S$ est injective.

Remarque 1.3
Pour montrer qu’une application $f:E\to F$ est injective, on utilise souvent la contraposée de la définition : on montre que si $x,x’\in E$ et $x\neq x’$, alors on a $f(x)\neq f(x’)$. C’est ce que nous avons fait dans l’exemple précédent, mais il faut prendre garde que ce procédé s’appuie sur la logique classique naturelle et n’est pas transposable en logique intuitionniste.

Pour un exemple mathématique, tournons-vous vers les fonctions « puissance » :

Exemple 1.4
Si $n\in\mathbb N$, alors la fonction $f:x\in\mathbb R\mapsto x^n$ est injective si et seulement si $n$ est impair. Nous démontrerons ce résultat dans le cours sur les fonctions d’une variable réelle.

Pour les fonctions de $\mathbb R$ dans $\mathbb R$, on peut « visualiser » l’injectivité en considérant la représentation graphique : une application $f:\mathbb R\to\mathbb R$ est injective si et seulement si à chaque nombre réel $y\in\mathbb R$ il correspond au plus un seul point du graphe de $f$ d’ordonnée $y$ (voir les exercices). Ce point de vue est illustré sur la figure 12.

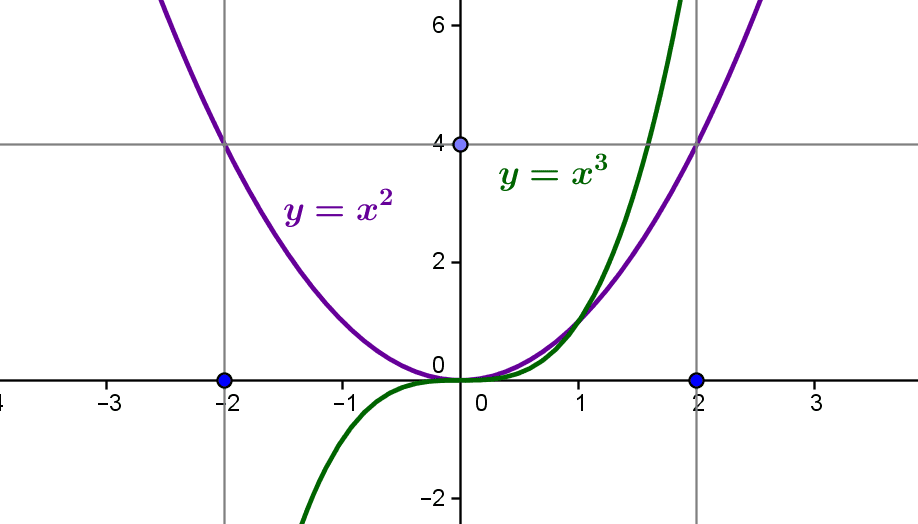
1.2. Le noyau d’une application

Si $f:E\to F$ est une application quelconque, il est possible de caractériser l’injectivité de $f$ (c’est-à-dire de donner une condition équivalente à cette propriété) grâce à une certaine relation binaire sur $E$, appelée noyau de $f$.

Définition 1.5
Le noyau de $f$ est l’ensemble $N$ des couples $(x,y)\in E\times E$ tels que $f(x)=f(y)$.

Le noyau d’une application est l’exemple typique de ce que nous appellerons une relation d’équivalence.

Il est évident que si $x\in E$, le couple $(x,x)$ est un élément de $N$, car $f(x)=f(x)$. Ainsi, le noyau de $f$ contient toujours l’ensemble des couples $(x,x)$, pour $x\in E$, ce qu’on appelle la {diagonale} du produit $E\times E$, notée souvent $\Delta_E$.

On peut alors caractériser les applications injectives grâce à cette diagonale, de la manière suivante :

Proposition 1.6
Une application $f:E\to F$ est injective si et seulement si le noyau $N$ de $f$ est la diagonale $\Delta_E$ de $E$.

Démonstration
Supposons que $f$ est injective, et montrons que $N=\Delta_E$ : comme $\Delta_E\subseteq N$, il suffit de montrer que $N\subseteq \Delta_E$. Soit donc $(x,y)\in N$ : par définition, du noyau, on a $f(x)=f(y)$, et comme $f$ est injective, on a $x=y$, si bien que $(x,y)=(x,x)$, donc $(x,y)\in \Delta_E$; on conclut que $N\subseteq\Delta_E$, d’où $N=\Delta_E$ par double inclusion.

Réciproquement, supposons que $N=\Delta_E$ et montrons que $f$ est injective : pour cela, soient $x,y\in E$ tels que $f(x)=f(y)$. Par définition du noyau, on a $(x,y)\in N$, et comme $N\subseteq \Delta_E$, on a $(x,y)\in \Delta_E$, soit $x=y$, si bien que $f$ est injective. $\square$

1.3. Applications surjectives

Reprenons l’exemple de l’application « addition » $+:\mathbb R\times\mathbb R\to\mathbb R$, de graphe $A\subseteq\mathbb R^2\times \mathbb R$.

Pour tout nombre réel $r$, il existe un couple de nombres réels $(x,y)\in\mathbb R^2$ tel que $x+y=r$, par exemple le couple $(0,r)$. Comme nous l’avons déjà évoqué, il peut exister plusieurs antécédents différents pour $r$ par l’addition (par exemple, $(r,0)$ et $(1,r-1)$ sont deux autres antécédents de $r$, puisque $r+0=r=1+(r-1)$), ce qui montre que $+$ n’est pas injective. Cependant, cette propriété, « duale » de l’existence systématique d’un correspondant par une application, mène à la définition suivante, qui formalise l’idée de {l’existence systématique d’un antécédent} par une application.

Définition 1.7
Une application $f:E\to F$ est dite surjective, ou une surjection, si pour tout $y\in F$, il existe (au moins un) $x\in E$ tel que $f(x)=y$, autrement dit si tout élément $y$ du co-domaine de $f$ possède un antécédent par $f$.

Nous avons donné l’addition en exemple, il est évident que la multiplication des nombres réels (ou même complexes) est également surjective (voir les exercices).

De même que le noyau d’une application est un ensemble particulier qui permet de caractériser les applications injectives, l’image d’une application (voir C1.II.1, section 6 : Image et image réciproque d’une partie, Définition 6.4) permet de caractériser les applications surjectives de manière simple.

Proposition 1.8
Une application $f:E\to F$ est surjective si et seulement si l’image de $f$ est $F$.

Démonstration
Supposons que $f$ soit surjective : si $y\in F$, il existe $x\in E$ tel que $f(x)=y$, si bien que $y\in Im(f)$, d’où $F=Im(f)$. Réciproquement si $F=Im(F)$, alors pour tout $y\in F$ on a $y\in Im(f)$ donc il existe $x\in E$ tel que $f(x)=y$, et $f$ est surjective. $\square$

Remarque 1.9
Le noyau et l’image d’une application ont des descriptions particulières en algèbre, ce que nous aurons l’occasion d’aborder dans les premiers cours d’algèbre (Semestre II), notamment à propos de la théorie des groupes et de la théorie des anneaux.

La figure suivante illustre la surjectivité des deux fonctions réciproques réelle exponentielle et logarithme.

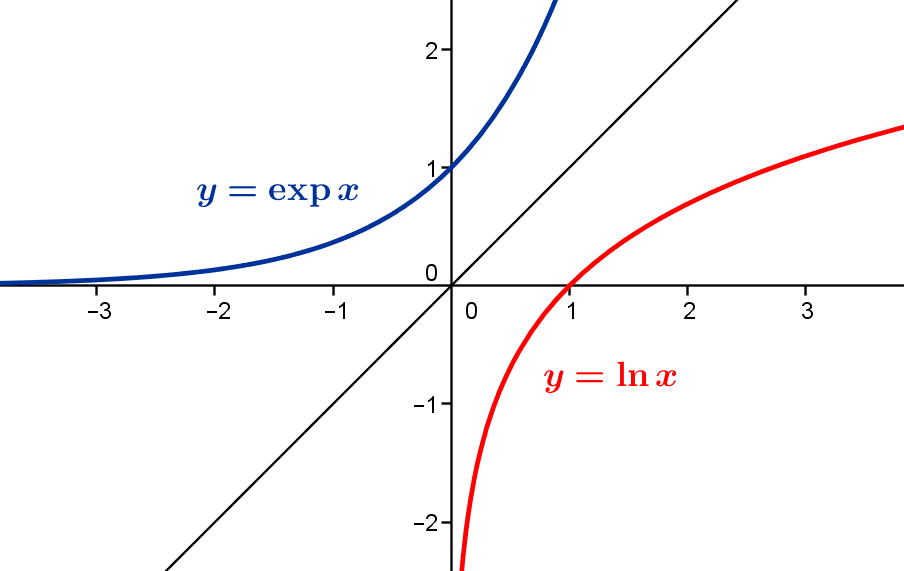
Mentionnons un cas très important d’application surjective. Si $E$ et $F$ sont deux ensembles non vides, on définit les projections $p:E\times F\to E$ (sur la première composante) et $q:E\times F\to F$ (sur la seconde composante) par $p(x,y)=x$ et $q(x,y)=y$ pour tout $(x,y)\in E\times F$.

Notons que si $E$ ou $F$ est vide, alors $E\times F$ est vide, et on peut encore définir $p:E\times F\to E$ et $q:E\times F\to F$ comme les applications vides de co-domaines respectifs $E$ et $F$, c’est-à-dire dont le graphe est l’ensemble vide (voir la section sur l’application vide).

Proposition 1.10
Si $E$ et $F$ ne sont pas vides, alors les projections $p:E\times F\to E$ et $q:E\times F\to F$ sont surjectives.

Démonstration
La démonstration est proposée dans les exercices.

1.4. Exercices

Les exercices de cette leçon sont courts mais nombreux. Ces notions sont tellement importantes qu’il est nécessaire de s’y arrêter un peu.

Exercice 1.11 [Applications injectives]
i) Montrer qu’une application $f=(E,F,R)$ est injective si et seulement si la relation inverse de $R$ est fonctionnelle.
ii) Montrer que l’application $m:\mathbb Z\to\mathbb Z$, $n\mapsto 2.n$ est injective.
iii) La fonction valeur absolue $\mathbb R\to\mathbb R$ est-elle injective ?
iv) Si $F$ est un ensemble, montrer que l’application vide $\emptyset\to F$ (c’est-à-dire à l’application dont le graphe est vide) est injective.
v) Si $E$ est un ensemble, montrer que l’application $E\to E\times E$, $x\mapsto (x,x)$, est injective.
vi) Si $f:E\to F$ est une application, soit $g$ la co-restriction de $f$ à l’image de $f$. Si $f$ est injective, montrer que $g$ est injective.
vii) Montrer que la composition de deux applications injectives est injective.

Exercice 1.12 [Applications surjectives]
i) La fonction partie entière $E:\mathbb R\to\mathbb Z$ est-elle surjective ?
ii) Si $F$ est un ensemble, à quelle condition l’application vide $\emptyset\to F$ est-elle surjective ?
iii) Si $E$ est un ensemble, montrer que l’application $E\to E\times E$, $x\mapsto (x,x)$ n’est pas surjective. Quelle est son image ?
iv) Si $E$ et $F$ sont deux ensembles non vides, notons $p:E\times F\to E$, $(x,y)\mapsto x$ et $q:E\times F\to F$, $(x,y)\mapsto y$ les deux {projections} du produit $E\times F$. Montrer que $p$ et $q$ sont surjectives.
v) Montrer que la multiplication $\times:\mathbb R\times\mathbb R\to\mathbb R$ est surjective.
vi) Si $f:E\to F$ est une application, soit $g$ la co-restriction de $f$ à l’image de $f$. Expliquer pourquoi $g$ est surjective.
vii) Montrer que la composition de deux applications surjectives est surjective.

2. Bijections et nombre d’éléments