by Jean Barbet | Feb 20, 2021 | Functions, Number Theory
Introduction When we introduced the circular exponential, the trigonometric functions cosine and sine were defined as its real part and imaginary part. From this, we derived the analytical expressions: \(\cos x=\sum_{n=0}^{+\infty} (-1)^n\dfrac{x^{2n}}{(2n)!}\) and...
by Jean Barbet | Feb 13, 2021 | Algebra, Geometry, Non classé
Introduction In Vector angles: geometric intuition and algebraic definition, we defined and described the group of Euclidean plane vector angles algebraically, using an equivalence relation on unit vectors. Just as we can measure lengths, we learn at primary school...
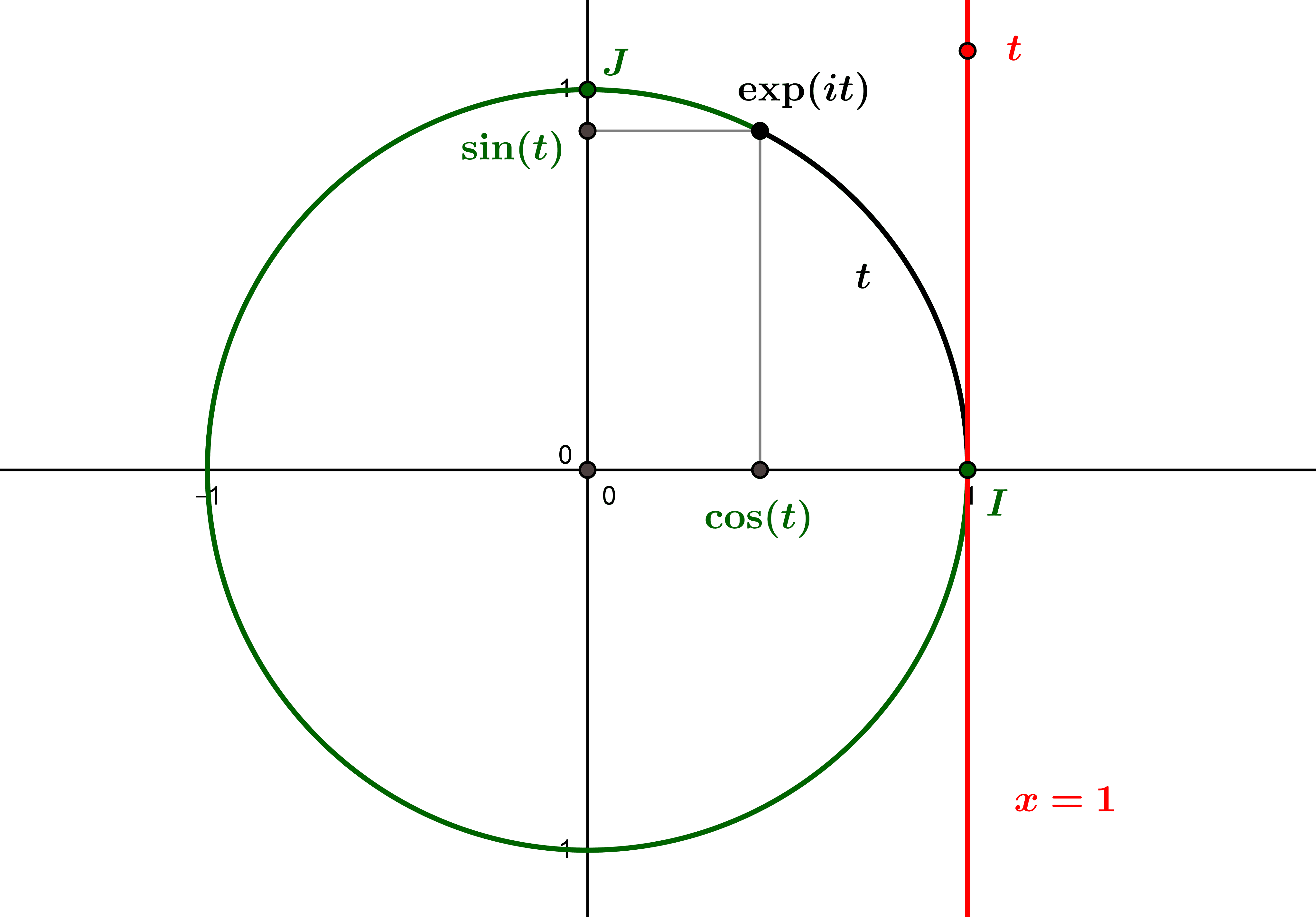
by Jean Barbet | Jan 9, 2021 | Analysis, Functions, Non classé
From the complex exponential function, we can define a “circular exponential” function, which “wraps” the real line around the trigonometric circle, and makes it possible to rigorously define the cosine and sine trigonometric functions, which...
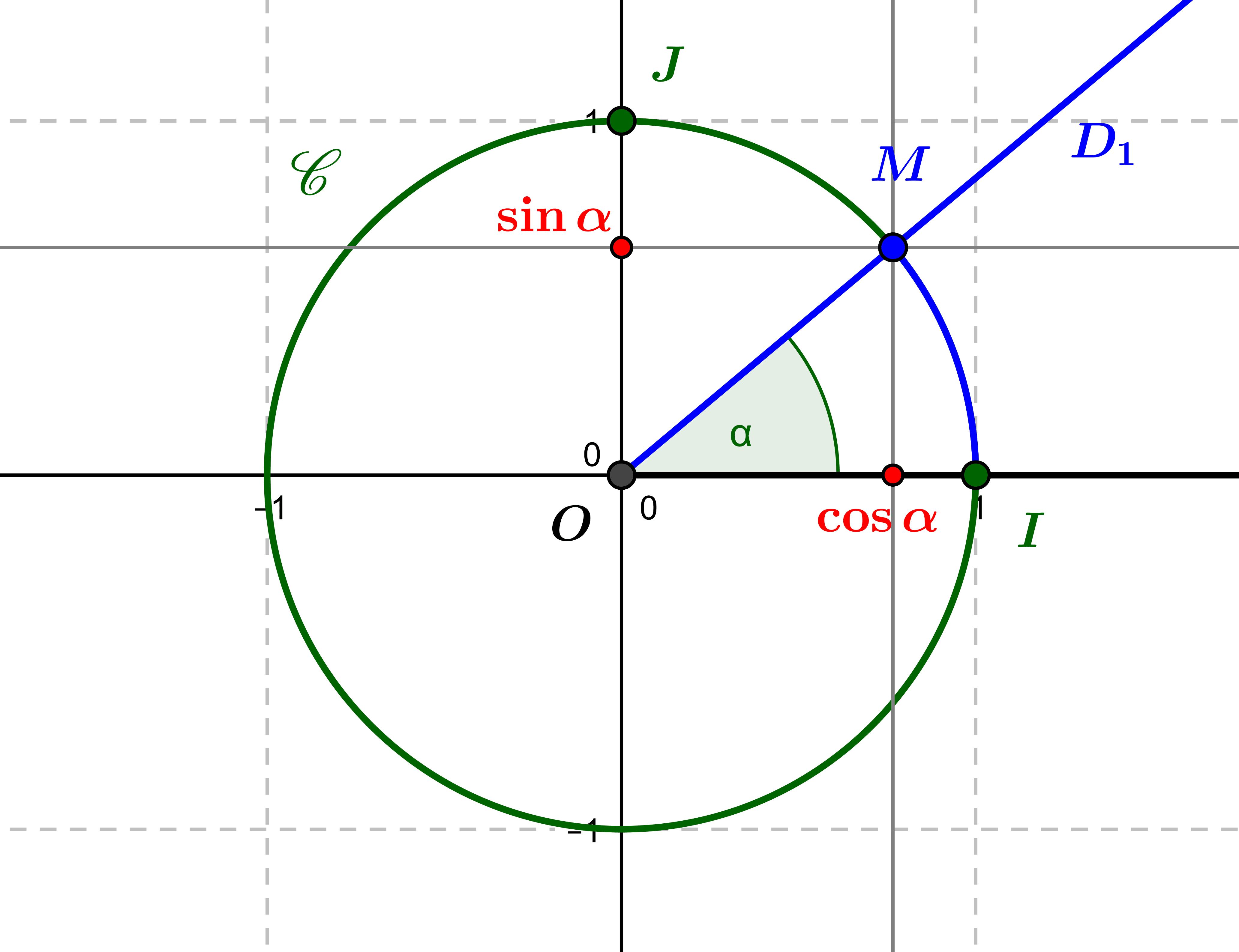
by Jean Barbet | Oct 25, 2020 | Geometry, Non classé, Trigonometry
The trigonometric circle allows us to define the cosine, sine and tangent of an oriented angle, and to give an interpretation through Thales’ and Pythagoras’ theorems. Introduction: trigonometry and functions Trigonometry is the study of the relationships...
