Le langage et l’expression mathématiques [C1.I.2]

1. Les types d’expressions mathématiques

Nous dirons en général qu’une locution du langage naturel est une expression mathématique si elle dénote un objet mathématique ou un état de choses (un fait) mathématique.

Parmi ces expressions nous distinguerons un petit nombre de types, qui sont les termes, les clauses, les énoncés, les définitions et les notations, que nous allons brièvement décrire.

1.1. Les termes

Les termes sont les expressions, littérales ou symboliques, qui dénotent les objets mathématiques, particuliers ou génériques.

Les termes sont en quelque sorte les « groupes nominaux » du discours mathématique, comparables aux noms propres lorsqu’ils dénotent des objets particuliers, aux noms communs lorsqu’ils dénotent des objets génériques.

Un terme dénote un objet générique quand il contient au moins une variable, c’est-à-dire une lettre ou un signe sans signification ou valeur fixée.

Un terme sans variable dénote un objet précis; un tel terme est dit clos ou fermé. Il est possible de substituer des termes aux variables dans d’autres termes, quand cela est approprié.

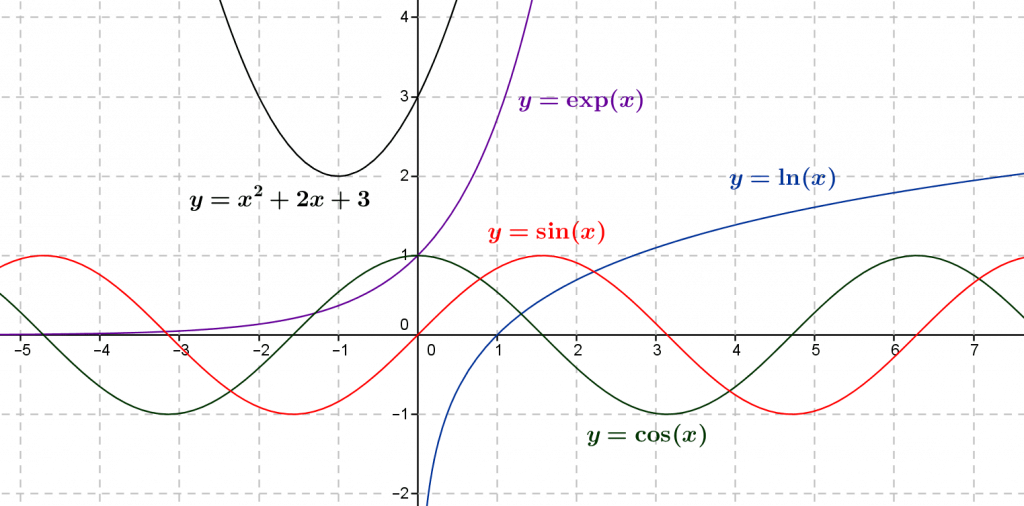
Exemple 1.1
i) Les expressions $0,1,\pi, e$ sont des termes qui dénotent des nombres particuliers ($e$ est la base de la fonction exponentielle).
ii) Les expressions $\cos x,\sin x, Log\ x, \exp x$ sont des termes qui dénotent des fonctions particulières (cosinus, sinus, logarithme et exponentielle). On note aussi $\ln$ le logarithme (dit népérien).
iii) Les expressions $\cos\ x,y+z,5x+12,Log\ u$ sont des termes qui dénotent des nombres génériques (le cosinus de $x$, la somme de $y$ et de $z$, la somme de $5$ fois $x$ et de $12$, le logarithme de $u$). Nous pouvons substituer le terme $\pi$ pour $x$ dans $\cos x$ pour obtenir le nombre réel $\cos \pi$, dont la valeur est $-1$.
iv) La fonction logarithme n’est définie que pour des nombres réels strictement positifs. Si $x\geq 0$, on a $5x+12>0$, donc il est possible de substituer le terme $5x+12$ pour $u$ dans $Log\ u$ pour obtenir le terme générique $Log(5x+12)$.
v) L’expression $x^2+2x+3$ est un terme qu’on appelle polynôme. Ces termes sont très importants en algèbre, où on les représente par les suites finies de leurs coefficients, ici $3,2,1$.

1.2 Les clauses

Les clauses sont les expressions, littérales ou symboliques, qui dénotent des états de choses (des faits) mathématiques, qu’ils soient particuliers ou génériques.

Une variable dans une clause est dite libre quand sa signification n’est pas déterminée à l’intérieur de la clause; autrement, elle est dite liée (ce deuxième cas apparaît avec la quantification, que nous introduirons bientôt).

Quand une clause contient au moins une variable libre, elle dénote une propriété générique des types d’objets dénotés par ses variables libres.

Quand elle ne contient aucune variable libre, nous l’appelons un énoncé et elle dénote une valeur de vérité, c’est-à-dire le « vrai » ou le « faux », selon la véracité de l’état de choses qu’elle exprime à propos des objets dont elle contient les signes.

Si $P$ ou $P(x)$ désigne une clause contenant une variable libre $x$, générique pour un ensemble $E$, et si $a$ est un élément de $E$, la substitution de $a$ pour $x$ dans $P$ est une clause (un énoncé si $x$ est la seule variable libre) que nous écrirons $P(a)$ ou $P(a/x)$.

Exemple 1.2
i) Si $a$ n’est pas un objet précis dans le contexte, la clause « $a<5$ » possède une variable libre $a$ et exprime que $a$ est (strictement) inférieur à $5$. Si on substitue un nombre approprié à $a$, cette clause se transforme est un énoncé qui est vrai ou faux selon la valeur attribuée à $a$. Par exemple, si on remplace $a$ par $2$ (on dit parfois qu’on « pose » $a=2$), alors la clause devient $2<5$, laquelle est vraie; tandis que si l’on pose $a=2\pi$, elle devient $2\pi<5$, ce qui est faux.
ii) La clause « $\forall x\in\mathbb N,\ 0<x$ » se traduit par « pour tout nombre entier naturel $x$, on a $0<x$ ». Bien qu’elle contienne la variable $x$, cette variable n’est pas libre, car on ne peut lui assigner une valeur : son « sens » est lié à la quantification « pour tout ». Cette clause est donc un énoncé, et dénote le faux, parce que $0$ n’est pas strictement inférieur à lui-même.
iii) L’expression « $m$ est un multiple de $n$ », où $m$ et $n$ sont deux variables qui dénotent des entiers naturels, est une clause mathématique avec deux variables libres, $m$ and $n$. Elle peut se reformuler comme : « il existe un entier naturel $d$ tel que $m=n\times d$ », symboliquement $\exists d\in\mathbb N, m=n\times d$, où $d$ est une variable « auxiliaire », quantifiée existentiellement et donc liée (nous parlerons bientôt en détail de la quantification).

Parmi les clauses, nous distinguerons les clauses élémentaires, qui expriment des relations mathématiques simples entre les objets qu’elles contiennent.

Exemple 1.3
i) La clause « $a<5$ » est élémentaire, ainsi que les clauses « $0=7$ » et « $(5\times 12)+(-\pi)>Log(e+19)$ ».
ii) La clause « $\forall x\in \mathbb N,\ 0<x$ » n’est pas élémentaire, car elle est construite à partir de la clause élémentaire « $0<x$ » par l’utilisation d’une quantification (universelle).
iii) La clause « $m=n\times d$ » est élémentaire, mais la clause « $\exists d,m=n\times d$ » qui exprime que $m$ est un multiple de $n$, ne l’est pas. Cependant, si nous introduisons la notation (standard) « $n|m$ » (qui se lit « $n$ divise $m$ ») pour la relation « $m$ est un multiple de $n$ », la clause $n|m$ est élémentaire. Le caractère élémentaire d’une clause dépend donc du vocabulaire symbolique que nous utilisons, et donc du contexte.

Lorsqu’on substitue des termes à toutes les variables libres d’une clause, on obtient une nouvelle clause. Si tous les termes substitués sont clos, cette opération transforme la clause d’origine, qui possède une signification « ouverte » en un énoncé, qui est soit vrai soit faux, selon la substitution opérée.

Exemple 1.4
i) Dans la clause « $x<y$ », si nous remplaçons $x$ par $\pi$ et $y$ par $2$, nous obtenons l’énoncé $\pi<2$, qui est faux. Si nous remplaçons cependant $x$ par $10$ et $y$ par $10^{10}$, nous obtenons un énoncé vrai.
ii) Dans la clause « $\forall x\in\mathbb N,\ y\leq x$ », où $y$ est la seule variable libre, si nous remplaçons $y$ par $0$, nous obtenons un énoncé vrai, tandis que si nous remplaçons $y$ par tout autre entier naturel, nous obtenons un énoncé faux.
iii) Dans la clause « $n|m$ », si nous remplaçons $n$ par $2$ et $m$ par $6$, nous obtenons un énoncé vrai, si nous remplaçons $n$ par $17$ et $m$ par $23$, nous obtenons un énoncé faux. Si nous remplaçons $n$ et $m$ par des entiers naturels tels que $n>m$, nous obtenons toujours un énoncé faux (nous prouverons ceci plus tard).

1.3. Les définitions et les notations

Les définitions sont les expressions mathématiques qui introduisent de nouveaux objets ou de nouvelles notions, à partir d’objets déjà connus ou définis, et de leurs propriétés.

Exemple 1.5
Voici quelques exemples de définitions. L’étudiant(e) ou la lectrice n’est pas censé(e) tout connaître.
i) Un nombre réel $x$ est dit positif s’il est supérieur à $0$, symboliquement si $x\geq 0$.
ii) Une fonction $f:[a,b]\to \mathbb R$ est dite intégrable (au sens de Riemann) si le supremum et l’infimum de l’ensemble des intégrales de fonctions en escaliers qui respectivement minorent et majorent $f$, coïncident. Leur valeur commune est alors appelée intégrale (de Riemann) de $f$ entre $a$ et $b$.
iii) Si $m$ et $n$ sont des entiers naturels, on dit que $m$ divise $n$ si il existe un entier naturel $d$ tel que $n=m.d$ (la multiplication se note souvent par un point).

Les notations sont les expressions mathématiques qui introduisent un nouveau symbole pour un objet bien défini, particulier ou générique, et souvent en même temps que la définition de cet objet.

Exemple 1.6
Voici quelques exemples contenant une notation.
i) Soit $E$ un ensemble.
ii) Si $f:[a,b]\to \mathbb R$ est intégrable au sens de Riemann, on note $\int_a^b f(t)\ dt$ l’intégrale de $f$ entre $a$ et $b$.
iii) On note $m|n$ la relation « $m$ divise $n$ ».

Remarque 1.7
Les notations peuvent être utilisées de deux façons : soit pour désigner de manière durable une notion clairement définie, comme dans les clauses (ii) et (iii) de l’exemple précédent, soit comme une désignation accessoire dans le flux du discours mathématique, comme dans la clause (i), pour une explication ou une démonstration par exemple.

2. Les opérations logiques sur les clauses

4. La quantification des clauses mathématiques

4.1. Principe de la quantification mathématique

La théorie des ensembles étant la trame conceptuelle de la mathématique, toutes les clauses mathématiques se ramènent essentiellement à des clauses « construites » à partir de clauses élémentaires, grâce aux opérations précédentes et ce qu’on appelle les quantifications.

En effet, les propriétés mathématiques d’un objet particulier ou générique sont décrites en relation à d’autres objets, et à l’intérieur de certains ensembles.

A cause de l’universalité de la méta-relation $\in$ entre les objets et les ensembles, pour obtenir toute la puissance expressive du langage mathématique il n’est nécessaire de compléter la combinaison des clauses élémentaires par les opérations logiques que par l’information concernant l’existence d’un objet ayant une « sous-propriété » ou l’universalité des objets ayant une telle sous-propriété. Par une « sous-propriété », nous entendons de manière informelle une propriété décrite par une partie d’une clause.

Exemple 4.1
Si $P$ est la clause « $x\geq 0$ et $x^2\neq 5$ », alors les clauses « $x\geq 0$ » et « $x^2\neq 5$ » expriment des sous-propriétés de la propriété générique exprimée par $P$.

Si l’on considère la propriété $P$ de l’exemple, il est naturel de se poser deux questions :
– existe-t-il un nombre réel $a$ ayant la propriété $P$ (c’est-à-dire tel que $P(a/x)$ est vrai) ?
– tous les nombres réels $a$ ont-ils la propriété $P$ ?

Ces deux possibilités correspondent aux deux types de quantifications, existentielle et universelle, et l’expression de ces deux types de faits suffit à compléter notre description du langage mathématique.

La quantification n’est pas un artifice de la science mathématique : elle correspond à l’addition de l’adverbe « tous » ou « tout » dans les expressions naturelles (pour la quantification universelle), ou de l’adverbe « certains » ou « certain » pour la quantification existentielle.

Ces deux quantifications étaient déjà bien connues dans l’Antiquité grecque; on les retrouve notamment chez Aristote, et à travers son héritage dans la logique de la scolastique médiévale.

Exemple 4.2
Un exemple de ces quantifications naturelles tiré de l’ancienne logique grecque (Aristote) est le suivant : « tous les hommes sont mortels ». Ici, l’expression « les hommes sont mortels » est complétée par le « quantificateur ‘tous' ». L’analogue pour le quantificateur existentiel est l’expression « certains hommes sont mortels ». La négation naturelle de « tous les hommes sont mortels » est « certains hommes ne sont pas mortels »; il existe une relation essentielle entre ces deux quantifications, liée à la négation, que nous aborderons ici dans le cadre mathématique propre.

Nous avons déjà vu des exemples de quantifications, et ils montrent que les énoncés mathématiques « intéressants » doivent souvent être construits à partir de clauses élémentaires contenant des variables libres, de manière à pouvoir affirmer quelque chose de plus élaboré que de simples relations particulières (même si certaines équations, entre nombres et fonctions par exemple, ont un intérêt mathématique essentiel; par exemple, l’étudiant(e) ou le lecteur pourra comprendre à son niveau, à la fin du semestre, la formule d’Euler, soit $e^{i\pi}+1=0$).

Nous avons aussi utilisé la quantification pour introduire des définitions, comme dans l’exemple de la divisibilité. Il s’agit donc d’un mode ubiquitaire de « transformation » des expressions mathématiques, qui « ferme » les clauses par rapport aux variables qu’elles contiennent.

4.2. La quantification existentielle

Si $P$ est une clause et $x$ une variable pour les éléments d’un ensemble $E$, la quantification existentielle de $P$ par $x$, notée « $\exists x\in E,\ P$ » (lire « il existe $x\in E$ tel que $P$ »), est la clause dont la signification est « il existe au moins un élément $a$ de $E$ tel que la clause obtenue en remplaçant $x$ par $a$ dans $P$, est valide ».

Remarque 4.3
i) La notation de la quantification peut varier selon les textes mathématiques : par exemple, on pourra écrire $(\exists x\in E)\ P$ pour $\exists x\in E,\ P$. En général, il n’y a aucune difficulté pour s’adapter à ces variations mineures : l’important est l’usage du symbole $\exists$.
ii) Il se peut que la variable $x$ n’apparaisse pas dans $P$, ou que $P$ possède d’autres variables libres que $x$ : nous ne présageons rien à ce sujet.

Si $x$ est la seule variable libre de $P$, alors la clause « $\exists x\in E,\ P$ » est un énoncé qui par définition est vrai exactement lorsqu’il existe un élément $a$ de $E$ tel que l’énoncé $P(a/x)$ est vrai. Cet énoncé est faux exactement lorsque pour aucun élément $a$ de $E$, l’énoncé $P(a/x)$ n’est vrai.

Exemple 4.4
i) Si $m$ et $n$ dénotent des entiers relatifs génériques, la relation « $m$ divise $n$ » (« $m|n$ ») a été définie par une quantification existentielle. En effet, si $P$ est la clause « $m.d=n$ », où $d$ est une nouvelle variable générique pour un entier relatif, la relation $m|n$ est définie par la clause $\exists d\in\mathbb Z,\ P$, soit « $\exists d\in\mathbb Z,\ m.d=n$ », dont la signification intuitive est qu’il existe un entier relatif $d$ pour lequel $m.d=n$, ce qui traduit effectivement l’idée que $n$ est un multiple de $m$.
ii) Si $x$ est une variable pour un nombre réel, nous avons affirmé dans la leçon précédente que la clause $P$ : « $x\geq 0$ » est équivalente à $Q$ : « $x$ est un carré » (c’est une propriété de l’ensemble $\mathbb R$, que nous démontrerons ultérieurement). L’expression rigoureuse de $Q$ se fait à l’aide d’un quantificateur existentiel, sous la forme « $\exists y\in\mathbb R,\ y^2=x$ », clause comprenant la variable libre $x$ et la variable $y$ pour un nombre réel, quantifiée existentiellement.
iii) Si $m$ et $n$ dénotent des entiers naturels génériques, la relation habituelle $m\leq n$ peut se définir à partir de l’addition et d’une quantification existentielle, par la clause $\exists p\in\mathbb N,\ m+p=n$, pour $p$ une nouvelle variable pour un entier naturel. Noter l’analogie avec la définition de la divisibilité.

Remarque 4.5
Lorsqu’on écrit une clause sous forme symbolique, on ne précise pas les ensembles correspondants aux éléments génériques dénotés par les variables libres : cela est précisé dans le contexte. Par contraste, sous la forme dans laquelle nous présentons ici la quantification, on a tendance à écrire l’ensemble correspondant à chaque variable quantifiée (« $\exists x\in E,\ P$ » plutôt que « $\exists x\ P$ »). Il n’est cependant pas interdit d’omettre l’ensemble de référence dans la quantification, surtout lorsque toutes les variables se rapportent au même ensemble. Le symbolisme n’est pas forcément synonyme de formalisme.

4.3. La quantification universelle

Si $P$ est une clause et $x$ une variable pour les éléments d’un ensemble $E$, la \emph{quantification universelle de $P$ par $x$, notée « $\forall x\in E,\ P$ » (lire « pour tout $x\in E$, $P$ ») est la clause dont la signification est « pour tous les éléments $a$ de $E$, la clause obtenue en substituant $x$ par $a$ dans $P$, est valide ».

Remarque 4.6
Comme pour la quantification existentielle, on peut trouver des variations de cette notation, que nous emploierons occasionnellement, comme par exemple $(\forall x\in E)\ P$.

Si $x$ est la seule variable libre de $P$, alors la clause « $\forall x\in E,\ P$ » est un énoncé qui est vrai exactement lorsque pour tout élément $a$ de $E$, l’énoncé $P(a/x)$ est vrai. Il est donc faux exactement lorsqu’il existe un élément $a$ de $E$ pour lequel $P(a/x)$ est faux (c’est la version mathématique de « tous les hommes sont mortels »).

On voit ainsi qu’il existe une « dualité » entre la quantification existentielle et la quantification universelle, qui passe par la négation et est analogue d’une dualité entre la disjonction et la conjonction. Nous aurons l’occasion d’y revenir dans deux sections.

Remarque 4.7
De manière analogue au rapport existant entre l’équivalence logique et la validité universelle de l’équivalence de deux clauses, il existe un rapport entre la quantification universelle et la validité universelle. Si $P$ est une clause possédant une unique variable libre $x$ pour les éléments d’un ensemble $E$, alors $P$ est universellement valide si et seulement si l’énoncé « $\forall x\in E,\ P$ » est vrai, ce qui découle immédiatement des définitions.

Exemple 4.8
i) Si $P$ est la clause « $(x\geq 0)\Rightarrow(\exists y\in\mathbb R,\ y^2=x)$ », avec $x$ un nombre réel générique (« si $x$ est positif, alors $x$ est un carré), alors l’énoncé $\forall x,\ P$ est vrai car $P$ est universellement valide (voir l’exemple précédent).
ii) Un entier naturel $p$ est appelé un nombre premier s’il est différent de $1$ et n’est divisible que par $1$ et lui-même. On peut exprimer cette propriété par la clause suivante, un peu complexe, où $p$ est un entier naturel générique : « $(p\neq 1)\wedge (\forall n\in\mathbb N,n|p\Rightarrow((n=1)\vee (n=p)))$ ». C’est un bon exercice que de décomposer cette écriture symbolique pour comprendre pourquoi elle exprime que $p$ est un nombre premier.
iii) Contrairement aux nombres réels, tout nombre complexe possède une racine carrée ! Ceci peut s’exprimer symboliquement par l’énoncé « $\forall z\in \mathbb C,\exists w\in \mathbb C,\ w^2=z$ ». On observe ici une combinaison des deux types de quantification.

4.4. Exercices

Exercice 4.9
i) Utiliser une quantification existentielle pour exprimer la relation $m<n$ entre deux entiers naturels à partir de la seule addition et du nombre $1$.
ii) L’énoncé $\exists x,\ x^2=2$, où $x$ dénote un nombre réel générique, est-il vrai ?
iii) Exprimer symboliquement la propriété « $0$ est le plus petit entier naturel » (c’est-à-dire : « $0$ est inférieur à tout entier naturel ») à l’aide de la relation $\leq$ et d’une quantification universelle.
iv) Ecrire un énoncé faux comportant une quantification universelle.

5. Relations entre les opérations logiques simples

5.1. Le jeu des opérations logiques et la négation